Distribució gaussiana inversa generalitzada

Generalized inverse Gaussian

Funció de densitat de probabilitat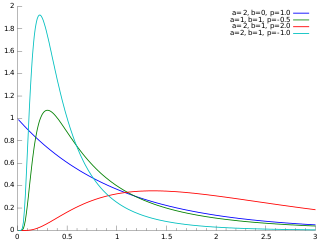
Tipus	família exponencial i distribució de probabilitat contínua
Epònim	Carl Friedrich Gauß i Herbert Sichel (en)
Paràmetres	a > 0, b > 0, p real
Suport	x > 0
fdp	${\displaystyle f(x)={\frac {(a/b)^{p/2}}{2K_{p}({\sqrt {ab}})}}x^{(p-1)}e^{-(ax+b/x)/2}}$
Variància	${\displaystyle \left({\frac {b}{a}}\right)\left[{\frac {K_{p+2}({\sqrt {ab}})}{K_{p}({\sqrt {ab}})}}-\left({\frac {K_{p+1}({\sqrt {ab}})}{K_{p}({\sqrt {ab}})}}\right)^{2}\right]}$

En teoria i estadística de probabilitats, la distribució gaussiana inversa generalitzada (GIG) és una família de tres paràmetres de distribucions de probabilitat contínues amb funció de densitat de probabilitat.

${\displaystyle f(x)={\frac {(a/b)^{p/2}}{2K_{p}({\sqrt {ab}})}}x^{(p-1)}e^{-(ax+b/x)/2},\qquad x>0,}$

on K_p és una funció de Bessel modificada del segon tipus, a > 0, b > 0 i p un paràmetre real. S'utilitza àmpliament en geoestadística, lingüística estadística, finances, etc. Aquesta distribució va ser proposada per primera vegada per Étienne Halphen.^[1][2] Va ser redescoberta i popularitzada per Ole Barndorff-Nielsen, que la va anomenar distribució gaussiana inversa generalitzada. Les seves propietats estadístiques es discuteixen a les notes de la conferència de Bent Jørgensen.^[3]

Propietats

Per fixació ${\displaystyle \theta ={\sqrt {ab}}}$ i ${\displaystyle \eta ={\sqrt {b/a}}}$, podem expressar alternativament la distribució GIG com ${\displaystyle f(x)={\frac {1}{2\eta K_{p}(\theta )}}\left({\frac {x}{\eta }}\right)^{p-1}e^{-\theta (x/\eta +\eta /x)/2},}$on ${\displaystyle \theta }$ és el paràmetre de concentració mentre ${\displaystyle \eta }$ és el paràmetre d'escala.

Barndorff-Nielsen i Halgreen van demostrar que la distribució GIG és infinitament divisible.

Característica d'una variable aleatòria ${\displaystyle X\sim GIG(p,a,b)}$ es dona com (per a una derivació de la funció característica, vegeu materials suplementaris de^[4])

${\displaystyle E(e^{itX})=\left({\frac {a}{a-2it}}\right)^{\frac {p}{2}}{\frac {K_{p}\left({\sqrt {(a-2it)b}}\right)}{K_{p}\left({\sqrt {ab}}\right)}}}$

per ${\displaystyle t\in \mathbb {R} }$ on ${\displaystyle i}$ denota el nombre imaginari.

Referències