Nichtnegative Matrixfaktorisierung

Die Nichtnegative Matrixfaktorisierung (NMF) ist ein Verfahren zur Dimensionsreduktion von Daten. Eine Matrix mit Einträgen in den nichtnegativen reellen Zahlen wird dabei linear in Faktoren vom Rang 1 zerlegt. Durch spezielle Algorithmen kann eine Zerlegung gefunden werden, bei der auch die einzelnen Faktoren nichtnegativ sind. Diese Forderung führt in vielen Fällen zu Zerlegungen, die leichter zu interpretieren sind und die Daten als Summe von klar getrennten Komponenten darstellen. Die NMF wird seit ihrer Einführung 1999^[1] in vielen Gebieten der Wissenschaft angewandt.

In der Chemometrik ist die nichtnegative Matrixfaktorisierung bereits seit den 1970er Jahren bekannt, wobei sie allerdings nicht als Faktorisierung von Matrizen beschrieben wurde. In den 90er Jahren veröffentlichten einige finnische Wissenschaftler Arbeiten zur positiven Matrixfaktorisierung.^[2]

Den Durchbruch zur weiteren Verbreitung schaffte die NMF, als die amerikanischen Neurowissenschaftler Daniel D. Lee und Sebastian Seung 1999 in einem Artikel in der Fachzeitschrift Nature^[1] ihre Eigenschaften untersuchten und den einfachen multiplikativen Algorithmus zu ihrer Berechnung angaben. Die Faktorisierung erfreut sich seitdem großer Beliebtheit und es sind mathematische Analysen, neue Berechnungsalgorithmen und abgewandelte Faktorisierungen^[3][4] entstanden.

Sei ${\displaystyle X}$ eine beliebige Matrix der Dimension ${\displaystyle m\times n}$ mit nichtnegativen Einträgen. Weiterhin sei die Anzahl der Komponenten ${\displaystyle k\in \mathbb {N} }$ gegeben, die kleiner als ${\displaystyle m}$ und als ${\displaystyle n}$ sei. Die nichtnegative Matrixfaktorisierung besteht dann aus einer Matrix ${\displaystyle W}$ der Dimension ${\displaystyle m\times k}$ und einer Matrix ${\displaystyle H}$ der Dimension ${\displaystyle k\times n}$, die beide nichtnegative Einträge besitzen und gemeinsam die Frobeniusnorm der Differenz

${\displaystyle \lVert X-WH\rVert _{\text{fro}}}$

minimieren.

Diese Definition entspricht, abgesehen von der Forderung der Nichtnegativität, genau der der Hauptkomponentenanalyse. Die Faktorisierung ist durch das Minimierungsproblem nicht eindeutig bestimmt. Beispielsweise sind für eine Permutationsmatrix ${\displaystyle \Pi \in S_{k}}$ die Matrizen ${\displaystyle W'=W\Pi }$ und ${\displaystyle H'=\Pi ^{-1}H}$ ebenfalls Minimierer von ${\displaystyle \lVert X-W'H'\rVert _{\text{fro}}}$, sodass die Ordnung der Faktoren also völlig unbestimmt ist. Auch die Skalierung der Faktoren kann variieren.

Das folgende Beispiel zeigt, wie man mithilfe der NMF zum Beispiel die Aktivität von Neuronen analysieren kann. Als Ausgangsmatrix ${\displaystyle X}$ wählen wir eine Matrix, die durch Helligkeitswerte in dem rechts stehenden Video gegeben ist. Das Video zeigt eine optogenetische Aufnahme aus dem Gehirn einer Maus; die Maus wurde also gentechnisch so verändert, dass die Aktivierung der Kalziumkanäle der Neuronen einen Lichtimpuls verursacht.

Die Zeilen der Matrix sollen nun die einzelnen Zeitpunkte darstellen, die Spalten die einzelnen Bildpunkte (Pixel) des Videos. Da das Video aus 400 Einzelbildern besteht, die jeweils ${\displaystyle 512\times 512}$ Pixel groß sind, ergibt sich so eine Matrix der Dimension ${\displaystyle 400\times 262\,144}$.

Als Komponentenanzahl wählen wir ${\displaystyle k=6}$. Die nichtnegative Matrix ${\displaystyle W}$ der Dimension ${\displaystyle 400\times 6}$ gibt dann den Zeit-Faktor an, die Matrix ${\displaystyle H}$ der Dimension ${\displaystyle 6\times 262\,144}$ beschreibt die räumliche Verteilung. Die Zeilen der Matrix ${\displaystyle H}$ können dann wieder zu Bildern aufgefaltet werden. Es ergeben sich die folgenden Faktoren:

• 
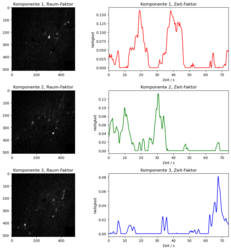  Ergebnis der NMF sind sechs Komponenten, die jeweils einen zeitlichen und einen räumlichen Faktor haben. Hier sind drei Komponenten gezeigt, die jeweils Gruppen von gemeinsam feuernden Neuronen darzustellen scheinen.
• 
  Die räumlichen Faktoren können auch räumlich überlagert dargestellt werden (hier als Farbkanäle eines RGB-Bildes), um die Neuronen visuell in funktional ähnliche Klassen einzuteilen

Die Matrixfaktorisierung kann somit aufzeigen, dass bestimmte Gruppen von Neuronen gemeinsam feuern. Dass die Gewichtungen nichtnegativ sind, ist hier klar von Vorteil, denn die Faktoren sind leichter interpretierbar, wenn keine Neuronen negativ gewichtet werden.

Lee und Seung gaben folgende multiplikative Update-Regel zur Bestimmung von ${\displaystyle W}$ und ${\displaystyle H}$ an:

${\displaystyle H\leftarrow H\odot {\frac {W^{T}X}{W^{T}WH}}}$

${\displaystyle W\leftarrow W\odot {\frac {XH^{T}}{WHH^{T}}}}$

Hierbei bezeichnet ${\displaystyle \odot }$ das Hadamard-Produkt, also die elementweise Multiplikation, und auch bei den Brüchen sollen Zähler und Nenner in jedem Eintrag dividiert werden. Diese Update-Regeln kann aus dem Gradientenabstieg unter Hinzunahme spezieller Vorfaktoren hergeleitet werden. Der Vorteil eines multiplikativen gegenüber einem additiven Gradientenabstieg ist, dass die Faktoren automatisch das Vorzeichen beibehalten. Einer der Nachteile ist, dass Elemente von ${\displaystyle W}$ oder ${\displaystyle H}$, die einmal null sind, nicht mehr positiv werden können.

Ein anderes Verfahren zur Bestimmung von ${\displaystyle W}$ und ${\displaystyle H}$ ist die Methode der alternierenden Least-Squares-Näherungen. Während das Minimierungsproblem in ${\displaystyle W}$ und ${\displaystyle H}$ gemeinsam nicht konvex ist, ist das Minimieren von ${\displaystyle W}$ für gegebenes ${\displaystyle H}$ und andersherum ein konvexes Problem und damit leichter zu lösen. In der Tat handelt es sich bei der Minimierung von ${\displaystyle \lVert X-WH\rVert _{\text{fro}}}$ für festes ${\displaystyle H}$ einfach um ein least-squares-Regressionsproblem (kleinste-Quadrate-Regression), bis auf die Einschränkung, dass ${\displaystyle W}$ nichtnegativ sein muss. Für das Regressionsproblem mit nichtnegativen Variablen (NNLS, nonnegative least squares) gibt es zwar keine einfache analytische Darstellung, aber durchdachte Algorithmen, mit deren Hilfe das Optimierungsproblem dann gelöst werden kann. Die Kostenfunktion wird in jedem Schritt garantiert verringert. Die meisten Software-Pakete für die Nichtnegative Matrixfaktorisierung benutzen dieses Verfahren.^[6]

Da bei den iterativen Optimierungsverfahren nicht garantiert ist, dass sie ein globales Optimum finden, kann die Initialisierung der Faktoren ${\displaystyle W}$ und ${\displaystyle H}$ eine wichtige Rolle für das Endergebnis spielen. Statt einer zufälligen Initialisierung hat sich unter anderem die Initialisierung auf Grundlage einer zuvor ausgeführten Singulärwertzerlegung bewährt.

• Hauptkomponentenanalyse
• Unabhängigkeitsanalyse

• N. Gilis: Nonnegative Matrix Factorization. SIAM, 2020

1. ↑ ^{a b} Daniel D. Lee, H. Sebastian Seung: Learning the parts of objects by non-negative matrix factorization. In: Nature. Band 401, Nr. 6755, Oktober 1999, ISSN 1476-4687, S. 788–791, doi:10.1038/44565 (nature.com [abgerufen am 13. November 2022]). 
2. ↑ Pentti Paatero, Unto Tapper: Positive matrix factorization: A non-negative factor model with optimal utilization of error estimates of data values. In: Environmetrics. Band 5, Nr. 2, Juni 1994, S. 111–126, doi:10.1002/env.3170050203 (wiley.com [abgerufen am 13. November 2022]). 
3. ↑ C.H.Q. Ding, Tao Li, M.I. Jordan: Convex and Semi-Nonnegative Matrix Factorizations. In: IEEE Transactions on Pattern Analysis and Machine Intelligence. Band 32, Nr. 1, Januar 2010, ISSN 0162-8828, S. 45–55, doi:10.1109/TPAMI.2008.277 (ieee.org [abgerufen am 13. November 2022]). 
4. ↑ Paris Smaragdis: Non-negative Matrix Factor Deconvolution; Extraction of Multiple Sound Sources from Monophonic Inputs. In: Independent Component Analysis and Blind Signal Separation. Band 3195. Springer Berlin Heidelberg, Berlin, Heidelberg 2004, ISBN 3-540-23056-4, S. 494–499, doi:10.1007/978-3-540-30110-3_63 (springer.com [abgerufen am 13. November 2022]). 
5. ↑ Masashi Kondo, Kenta Kobayashi, Masamichi Ohkura, Junichi Nakai, Masanori Matsuzaki: Two-photon calcium imaging of the medial prefrontal cortex and hippocampus without cortical invasion. In: eLife. Band 6, 25. September 2017, ISSN 2050-084X, S. e26839, doi:10.7554/eLife.26839. 
6. ↑ Michael W. Berry, Murray Browne, Amy N. Langville, V. Paul Pauca, Robert J. Plemmons: Algorithms and applications for approximate nonnegative matrix factorization. In: Computational Statistics & Data Analysis. Band 52, Nr. 1, 15. September 2007, ISSN 0167-9473, S. 155–173, doi:10.1016/j.csda.2006.11.006 (sciencedirect.com [abgerufen am 13. November 2022]).