Satz von Descartes

In der Geometrie beschreibt der Satz von Descartes (Vier-Kreise-Satz von Descartes), benannt nach René Descartes, eine Beziehung zwischen vier Kreisen, die einander berühren. Der Satz kann dazu verwendet werden, zu drei sich gegenseitig berührenden Kreisen ein Paar der sogenannten vierten Kreise zu finden, welche ebenfalls die drei Kreise berühren. Nach Definition der vorzeichenbehafteten Krümmung ist der (kleinste) Kreis ${\displaystyle k_{4}}$ umringt von den drei gegebenen Kreisen (im Bild blau), hingegen sind sie vom (größten) Kreis ${\displaystyle k_{4}{'}}$ umschrieben (siehe Abschnitt Satz des Descartes).

Es handelt sich hier um einen Spezialfall des Apollonischen Problems. Berühren sich die gegebenen drei Kreise gegenseitig, sind zwei (ein Paar) apollonische Kreise (rot) möglich. Im Gegensatz dazu gibt es ohne gegenseitiger Berührung bis zu acht (vier Paare) apollonische Kreise.^[1]

Geschichte

Über geometrische Probleme im Zusammenhang mit Kreisen, die einander berühren, wurde schon vor mehr als 2000 Jahren nachgedacht. Im antiken Griechenland des 3. Jahrhunderts v. Chr. widmete Apollonios von Perge diesem Thema ein ganzes Buch. Unglücklicherweise ist uns dieses Werk mit dem Titel Über Berührungen nicht erhalten.

René Descartes erwähnte 1643 das Problem (gemäß den damaligen Gepflogenheiten) kurz in einem Brief an die Prinzessin Elisabeth von Böhmen. Er kam im Wesentlichen zu der Lösung, die weiter unten in Gleichung ${\displaystyle {\mathsf {(1)}}}$ beschrieben ist, auch wenn sein Beweis nicht korrekt war^[2]. Daher wird der Vier-Kreise-Satz heute nach Descartes benannt.

Der Satz wurde mehrfach unabhängig wiederentdeckt, unter anderem in einem Spezialfall in japanischen Tempelproblemen, von Jakob Steiner (1826), vom britischen Amateurmathematiker Philip Beecroft (1842)^[3] und von Frederick Soddy (1936). Man spricht manchmal von den Soddy-Kreisen, vielleicht weil Soddy seine Version des Satzes in Form eines Gedichts mit dem Titel The Kiss Precise veröffentlichte, das in der Zeitschrift Nature (20. Juni 1936) abgedruckt wurde.^[4] Soddy verallgemeinerte auch den Satz von Descartes zu einem Satz über Sphären im 3-dimensionalen Raum und Thorold Gosset auf n-Dimensionen.

Allan Wilks und Colin Mallows von den Bell Laboratories entdeckten Ende der 1990er Jahre, dass eine komplexe Version des Satzes von Descartes auch die Orte der Kreise festlegt. Näheres hierzu enthält der Abschnitt Komplexer Satz von Descartes.

Setzt man die Konstruktion fort, erhält man eine fraktale Struktur mit immer kleineren sich berührenden Kreisen. Während die ersten vier Krümmungen nach dem Satz von Descartes durch eine quadratische Gleichung verbunden sind, gilt für die folgenden Kreise eine lineare Gleichung. Startet man mit vier ganzzahligen Krümmungen, so haben auch die folgenden Krümmungen der Kreise in der Konstruktion ganzzahlige Werte. Die zahlentheoretischen Aspekte des Problems wurden insbesondere von Wilks, Jeffrey Lagarias, Ronald Graham, Peter Sarnak, Alex Kontorovich und Hee Oh weiter verfolgt.

Definition der vorzeichenbehafteten Krümmung

Der Satz von Descartes lässt sich am einfachsten durch den Begriff der Krümmung ausdrücken. Die vorzeichenbehaftete Krümmung eines Kreises wird definiert durch ${\displaystyle k=\pm 1/r}$, wobei r den Radius bezeichnet. Je größer der Kreis ist, desto kleiner ist der Betrag seiner Krümmung und umgekehrt.

Das Minuszeichen in ${\displaystyle k=\pm 1/r}$ gilt für einen Kreis, der die anderen drei Kreise einschließend berührt. Andernfalls ist das Pluszeichen zu setzen.

Betrachtet man eine Gerade als entarteten Kreis mit Krümmung ${\displaystyle k=0}$, so lässt sich der Satz von Descartes auch anwenden, wenn eine Gerade und zwei Kreise gegeben sind, die einander berühren, und ein dritter Kreis gesucht ist, der die Gerade und die gegebenen Kreise berührt.

Satz von Descartes

Gegeben seien vier einander berührende Kreise mit den Radien ${\displaystyle r_{1}}$, ${\displaystyle r_{2}}$, ${\displaystyle r_{3}}$ und ${\displaystyle r_{4}}$. Definiert man wie oben für jeden dieser Kreise die vorzeichenbehaftete Krümmung ${\displaystyle k_{i}}$ (für ${\displaystyle i=1,\ldots ,4}$), so ist folgende Gleichung erfüllt:^[5]

${\displaystyle {\mathsf {(1)}}\;(k_{1}+k_{2}+k_{3}+k_{4})^{2}=2\,(k_{1}^{2}+k_{2}^{2}+k_{3}^{2}+k_{4}^{2})}$

Auflösen dieser Gleichung nach ${\displaystyle k_{4}}$ ermöglicht es, den Radius des vierten Kreises zu bestimmen:

${\displaystyle {\mathsf {(2)}}\;k_{4}=k_{1}+k_{2}+k_{3}\pm 2{\sqrt {k_{1}k_{2}+k_{2}k_{3}+k_{3}k_{1}}}.}$

Das Plus-Minus-Symbol drückt aus, dass es im Allgemeinen zwei Lösungen gibt.

Beispiel

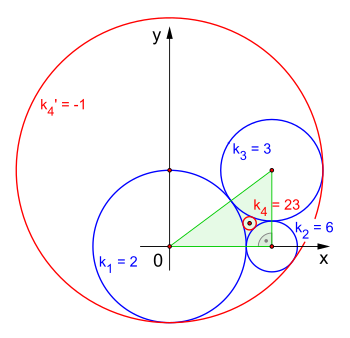
Gegeben seien drei Kreise mit den Radien ${\displaystyle r_{1}=1/2}$, ${\displaystyle r_{2}=1/6}$ und ${\displaystyle r_{3}=1/3}$. Dementsprechend hat die vorzeichenbehaftete Krümmung die Werte ${\displaystyle k_{1}=2}$, ${\displaystyle k_{2}=6}$ und ${\displaystyle k_{3}=3}$. Die Verbindung der Mittelpunkte dieser drei Kreise (blau) erzeugt ein rechtwinkliges Dreieck (hellgrün). Aus Gleichung ${\displaystyle {\mathsf {(2)}}}$ ergeben sich nun die beiden Lösungen ${\displaystyle k_{4}=23}$ und ${\displaystyle {k_{4}}'=-1}$. Der winzige Kreis (rot) zwischen den gegebenen Kreisen hat daher den Radius ${\displaystyle r_{4}=1/23}$. Der große Kreis (ebenfalls rot), der die gegebenen Kreise einschließt, hat den Radius ${\displaystyle {r_{4}}'=1}$. Da die Mittelpunkte der gegebenen Kreise ${\displaystyle k_{1},k_{2}}$ und ${\displaystyle k_{3}}$ auf den Eckpunkten eines rechtwinkligen Dreiecks liegen, ermöglicht dies die Festlegung der Kreise ${\displaystyle k_{4}}$ und ${\displaystyle k_{4}{'}}$ in einer einfachen Konstruktion (siehe Abschnitt Konstruktion mit Zirkel und Lineal). Alternativ kann, wie im Folgenden beschrieben, die exakte Position des Mittelpunktes des Kreises ${\displaystyle k_{4}}$ mithilfe eines kartesischen Koordinatensystems algebraisch bestimmt werden.

Aus den gegebenen Kreisradien erhält man die Koordinaten der (nicht bezeichneten) Mittelpunkte ${\displaystyle (M)}$: Kreis ${\displaystyle k_{1}}$ mit ${\displaystyle M_{k_{1}}=\left(0,0\right)}$, ${\displaystyle k_{2}}$ mit ${\displaystyle M_{k_{2}}=\left({\tfrac {2}{3}},0\right)}$ und ${\displaystyle k_{3}}$ mit ${\displaystyle M_{k_{3}}=\left({\tfrac {2}{3}},{\tfrac {1}{2}}\right)}$. Der Mittelpunkt des Kreises ${\displaystyle k_{4}}$ ist der Schnittpunkt zweier (nicht eingezeichneter) Hilfskreise ${\displaystyle H_{k1}}$ und ${\displaystyle H_{k2}}$. Für den Hilfskreis ${\displaystyle H_{k1}}$ um den Mittelpunkt des Kreises ${\displaystyle k_{1}}$ ergibt sich der Radius ${\displaystyle r_{Hk1}=\left({\tfrac {1}{2}}+{\tfrac {1}{23}}\right)={\tfrac {25}{46}}}$ und für ${\displaystyle H_{k2}}$ der Radius ${\displaystyle r_{Hk2}=\left({\tfrac {1}{6}}+{\tfrac {1}{23}}\right)={\tfrac {29}{138}}}$. Mit den nun bekannten Hilfskreisen ${\displaystyle H_{k1}}$ und ${\displaystyle H_{k2}}$ sind die Koordinaten des Mittelpunktes vom Kreis ${\displaystyle k_{4}}$ mit dem Ansatz Schnittpunkte zweier Kreise bestimmbar. Die nebenstehende Abbildung zeigt: Der Kreis ${\displaystyle k_{1}}$ hat den Nullpunkt als Mittelpunkt und der Kreis ${\displaystyle k_{2}}$ liegt auf der x-Achse. Für diesen Sonderfall gilt:

${\displaystyle x_{0}={\frac {r_{1}^{2}-r_{2}^{2}+x_{2}^{2}}{2x_{2}}}={\frac {\left({\frac {25}{46}}\right)^{2}-\left({\frac {29}{138}}\right)^{2}+\left({\frac {2}{3}}\right)^{2}}{\frac {4}{3}}}={\frac {12}{23}}}$,

${\displaystyle y_{0}={\sqrt {r_{1}^{2}-x_{0}^{2}}}={\sqrt {\left({\tfrac {25}{46}}\right)^{2}-\left({\tfrac {12}{23}}\right)^{2}}}={\frac {7}{46}}}$.

Somit hat der Mittelpunkt des kleinsten Kreises ${\displaystyle k_{4}}$ die Koordinaten ${\displaystyle M_{k_{4}}=\left({\tfrac {12}{23}},{\tfrac {7}{46}}\right)}$ und jener der die drei gegebenen Kreise einschließt ${\displaystyle k_{4}{'}}$ die Koordinaten ${\displaystyle M_{k_{4}{'}}=\left(0,{\tfrac {1}{2}}\right)}$.

Spezialfälle

Wird beispielsweise der dritte der drei gegebenen Kreise durch eine Gerade ersetzt, so wird ${\displaystyle k_{3}}$ gleich 0 und fällt aus Gleichung ${\displaystyle {\mathsf {(1)}}}$ heraus. Gleichung ${\displaystyle {\mathsf {(2)}}}$ wird in diesem Fall wesentlich einfacher:

${\displaystyle {\mathsf {(3)}}\;k_{4}=k_{1}+k_{2}\pm 2{\sqrt {k_{1}k_{2}}}.}$

Beispiel

Gegeben seien zwei Kreise mit den Radien ${\displaystyle r_{1}=1/4}$ und ${\displaystyle r_{2}=1/9}$ sowie eine Gerade, die als Kreis mit unendlichem Radius aufgefasst wird. Die entsprechenden Werte für die vorzeichenbehaftete Krümmung sind ${\displaystyle k_{1}=4}$, ${\displaystyle k_{2}=9}$ und ${\displaystyle k_{3}=0}$. Durch Anwendung von Gleichung ${\displaystyle {\mathsf {(3)}}}$ erhält man wieder zwei mögliche Werte, nämlich ${\displaystyle k_{4}=25}$ und ${\displaystyle {k_{4}}'=1}$. Für die Radien der beiden rot gezeichneten Kreise ergibt sich folglich ${\displaystyle r_{4}=1/25}$ beziehungsweise ${\displaystyle {r_{4}}'=1}$.

Der Satz von Descartes lässt sich nicht anwenden, wenn zwei oder sogar alle drei gegebenen Kreise durch Geraden ersetzt werden. Der Satz gilt auch dann nicht, wenn es mehr als einen einschließend berührenden Kreis gibt, also im Fall von drei ineinander gelegenen Kreisen mit gemeinsamem Berührpunkt.

Komplexer Satz von Descartes

Um einen Kreis vollständig zu bestimmen, nicht nur seinen Radius (oder seine Krümmung), muss man auch seinen Mittelpunkt kennen. Die Gleichung dafür lässt sich am einfachsten ausdrücken, wenn man die Koordinaten des Mittelpunkts (x, y) als komplexe Zahl ${\displaystyle z=x+iy}$ interpretiert. Die Gleichung für ${\displaystyle z_{1},z_{2},z_{3},z_{4}}$ ist dem Satz von Descartes sehr ähnlich und wird daher als komplexer Satz von Descartes bezeichnet.

Gegeben seien vier Kreise mit den Mittelpunkten ${\displaystyle z_{1},z_{2},z_{3},z_{4}}$ und den vorzeichenbehafteten Krümmungen ${\displaystyle k_{1},k_{2},k_{3},k_{4}}$ (siehe oben), die einander berühren. Dann gilt zusätzlich zu (1) die Beziehung

${\displaystyle {\mathsf {(4)}}\;(k_{1}z_{1}+k_{2}z_{2}+k_{3}z_{3}+k_{4}z_{4})^{2}=2\,(k_{1}^{2}z_{1}^{2}+k_{2}^{2}z_{2}^{2}+k_{3}^{2}z_{3}^{2}+k_{4}^{2}z_{4}^{2}).}$

Durch die Substitution ${\displaystyle q_{i}=k_{i}\cdot z_{i}}$ ergibt sich:

${\displaystyle {\mathsf {(5)}}\;(q_{1}+q_{2}+q_{3}+q_{4})^{2}=2\,(q_{1}^{2}+q_{2}^{2}+q_{3}^{2}+q_{4}^{2})}$

Diese Gleichung ist analog zu ${\displaystyle {\mathsf {(1)}}}$ und hat die Lösung:

${\displaystyle {\mathsf {(6)}}\;q_{4}=q_{1}+q_{2}+q_{3}\pm 2{\sqrt {q_{1}q_{2}+q_{2}q_{3}+q_{3}q_{1}}}.}$

Auch hier ergeben sich im Allgemeinen zwei Lösungen.

Hat man ${\displaystyle k_{4}}$ aus Gleichung ${\displaystyle {\mathsf {(2)}}}$ ermittelt, so erhält man ${\displaystyle z_{4}}$ durch ${\displaystyle z_{4}=q_{4}/k_{4}}$

Konstruktion mit Zirkel und Lineal

Allgemeiner Fall

Im allgemeinen Fall ergibt sich beim Verbinden der drei Mittelpunkte ein allgemeines Dreieck. Gegeben seien drei beliebige Kreise die zueinander tangential angeordnet sind. Gesucht sind die beiden Apollonios-Kreise mit ihren Mittelpunkten, genannt isoperimetrische Punkt bzw. Punkt des gleichen Umwegs. Apollonios von Perge zeigte erstmals, wie eine Lösung allein mit Zirkel und Lineal möglich ist.^[6] Das nebenstehende Bild zeigt eine Lösung nach Eppstein.^[7]

Es beginnt mit der Verbindung der Kreismittelpunkte. Das dabei entstehende allgemeine Dreieck ${\displaystyle ABC}$ bestimmt die drei Tangentenpunkte, auch Berührungspunkte (dunkelblau) genannt. Auf jede Dreiecksseite wird nun eine Senkrechte errichtet, die durch die gegenüberliegende Dreiecksecke (Kreismittelpunkt) und durch den Kreis verläuft. Dabei schneidet die Senkrechte den Kreis in zwei Punkten (hellgrün). Zieht man nun eine Gerade durch jeden dieser Schnittpunkte (hellgrün) und durch den Berührungspunkt (dunkelblau) der beiden anderen Kreise, liefert die Gerade zusätzlich zwei Berührungspunkte (rot), insgesamt bezeichnet mit ${\displaystyle D,\;E,\;F}$ und ${\displaystyle G,\;H,\;I}$. Der isoperimetrische Punkt ${\displaystyle P_{a}}$ sowie der Punkt des gleichen Umwegs ${\displaystyle P_{i}}$ werden mittels – nicht eingezeichneter – Mittelsenkrechten der Abstände ${\displaystyle |{\overline {EF}}|}$ und ${\displaystyle |{\overline {FD}}|}$ bzw. ${\displaystyle |{\overline {GH}}|}$ und ${\displaystyle |{\overline {HI}}|}$ bestimmt. Jetzt zieht man den Apollonios-Kreis mit den Berührungspunkten ${\displaystyle DFE}$ mit Radius ${\displaystyle |{\overline {P_{a}D}}|}$ um ${\displaystyle P_{a}}$ und schließlich den mit den Berührungspunkten ${\displaystyle GIH}$ mit Radius ${\displaystyle |{\overline {P_{i}G}}|}$ um ${\displaystyle P_{i}}$.^[7][8]

Kreismittelpunkte im rechtwinkligen Dreieck

Für die folgende Lösung sind zwei Gegebenheiten vorstellbar. Entweder die drei gegebenen Radien der Apollonios-Kreise entsprechen einem Pythagoreischen Tripel wie z. B. ${\displaystyle 3,\;4}$ und ${\displaystyle 5}$, dann liegen die drei Kreismittelpunkte bekanntlich in einem rechtwinkligen Dreieck oder es wird ein rechtwinkliges Dreieck mit beliebigen Seitenlängen – wie im Folgenden erläutert – gewählt.

Nach dem Einzeichnen des rechtwinkligen Dreiecks ${\displaystyle ABC}$ in beliebiger Lage und mit beliebigen Seitenlängen werden die Winkelhalbierenden ${\displaystyle wh_{1}}$ des Winkels ${\displaystyle CBA}$ sowie ${\displaystyle wh_{2}}$ des Winkels ${\displaystyle BAC}$ bestimmt. Sie schneiden sich im Mittelpunkt des Inkreises. Fällt man nun das Lot vom Inkreismittelpunkt beispielsweise auf die Dreiecksseite ${\displaystyle c}$, ergibt sich darauf der Berührungspunkt (dunkelblau) für die Kreise ${\displaystyle K1}$ und ${\displaystyle K2}$. Das Eintragen des Kreises ${\displaystyle K1}$ liefert den Berührungspunkt (dunkelblau) für den Kreis ${\displaystyle K3}$ und ermöglicht somit auch das Ziehen der Kreise ${\displaystyle K3}$ und ${\displaystyle K2}$. Es folgt eine Gerade durch die Dreiecksecke ${\displaystyle A}$ parallel zur Dreiecksseite ${\displaystyle a}$, eine zweite durch die Dreiecksecke ${\displaystyle B}$ parallel zur Dreiecksseite ${\displaystyle b}$ sowie die Verlängerung der Dreiecksseite ${\displaystyle b}$ bis zum Kreis ${\displaystyle K2}$. Schnittpunkte sind der isoperimetrische Punkt ${\displaystyle P_{a}}$, die Berührungspunkte ${\displaystyle D}$, ${\displaystyle E}$ auf ${\displaystyle K1}$ bzw. ${\displaystyle K2}$, Schnittpunkt ${\displaystyle F}$ sowie der hellgrüne Schnittpunkt auf ${\displaystyle K2}$ aus der Verlängerung der Dreiecksseite ${\displaystyle b.}$ Jetzt wird der Apollonios-Kreis um ${\displaystyle P_{a}}$ mit Radius ${\displaystyle |{\overline {P_{a}D}}|}$ eingetragen.

Um den Punkt des gleichen Umwegs ${\displaystyle P_{i}}$ sowie einen Berührungspunkt für den zweiten und letzten Apollonios-Kreis zu bestimmen, bedarf es zunächst einer Geraden. Sie geht durch den Schnittpunkt (hellgrün) des Kreises ${\displaystyle K2}$ und durch den Berührungspunkt (dunkelblau) der Kreise ${\displaystyle K1}$ und ${\displaystyle K3}$. Dabei schneidet sie im gesuchten Berührungspunkt ${\displaystyle G}$ den Kreis ${\displaystyle K2}$. Demzufolge ähnlich wie es bereits oben der allgemeine Fall verlangt. Weiters zieht man eine Halbgerade ab ${\displaystyle P_{a}}$ durch den Inkreismittelpunkt und eine zweite ab der Dreiecksecke ${\displaystyle A}$ durch den Berührungspunkt ${\displaystyle G}$ bis sich beide Halbgeraden im Punkt des gleichen Umwegs ${\displaystyle P_{i}}$ schneiden. Abschließend kann man den Apollonios-Kreis um ${\displaystyle P_{i}}$ mit Radius ${\displaystyle |{\overline {P_{i}G}}|}$ eintragen.

Verschiedenes

Die primitiven ganzzahligen Lösungen der vier Radien sind genau die Diagonalprodukte und Zeilenprodukte der beiden zwei-parametrigen Darstellungen der primitiven pythagoräischen Tripel, bspw. liefert das primitive pythagoräische Tripel ${\displaystyle (5,12,13)}$ mit den (als Spalten geschriebenen) Parameter-Darstellungen ${\displaystyle (2,3)^{T}}$ und ${\displaystyle (1=3-2,5=3+2)^{T}}$ die Diagonalprodukte ${\displaystyle 3,10}$ und die Zeilenprodukte ${\displaystyle 2,15}$, welche als Radien aufgefasst dem Satz von Descartes genügen.^[9][10]

Weblinks

• Jeffrey C. Lagarias, Colin L. Mallows, Allan R. Wilks: Beyond The Descartes Circle Theorem
• Dana Mackenzie A tisket, a Tasket, an Apollonian Gasket, American Scientist, Band 98, 2010, S. 10–14 (erhielt den Chauvenet-Preis 2015).

Einzelnachweise

1. ↑ David Gisch and Jason M. Ribando: Apollonios Problem: A study of solutions and their connections. (pdf) V. Connections and Extensions, Fig. 13. American Journal of Undergraduate Research, Band 3, 2004, Nr. 1, 29. Februar 2004, S. 23–24, archiviert vom Original (nicht mehr online verfügbar) am 15. April 2008; abgerufen am 9. Februar 2024 (englisch).  Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/www.ajur.uni.edu 
2. ↑ Dana Mackenzie, A tisket, a tasket, an Apollonian gasket, American Scientist, Band 98, 2010, S. 10–14
3. ↑ David Gisch and Jason M. Ribando: Apollonios Problem: A study of solutions and their connections. (pdf) II. The Euler-Gergonne-Soddy Triangle of a Triangle. American Journal of Undergraduate Research, Band 3, 2004, Nr. 1, 29. Februar 2004, S. 16, archiviert vom Original (nicht mehr online verfügbar) am 15. April 2008; abgerufen am 9. Februar 2024 (englisch).  Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/www.ajur.uni.edu 
4. ↑ David Gisch and Jason M. Ribando: Apollonios Problem: A study of solutions and their connections. (pdf) II. The Euler-Gergonne-Soddy Triangle of a Triangle. American Journal of Undergraduate Research, Band 3, 2004, Nr. 1, 29. Februar 2004, S. 17, archiviert vom Original (nicht mehr online verfügbar) am 15. April 2008; abgerufen am 9. Februar 2024 (englisch).  Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/www.ajur.uni.edu 
5. ↑ Frank Bernhart, H. Lee Price: Heron’s Formula, Descartes Circles, and Pythagorean Triangles. (PDF) 4 The Descartes Circle Theorem. arxiv, Cornell University, 1. Januar 2007, S. 8–9, abgerufen am 8. Februar 2024 (englisch). 
6. ↑ David Eppstein: Tangencies: Apollonian Circles. (pdf) University of California, Irvine, abgerufen am 17. Dezember 2023 (englisch). 
7. ↑ ^{a b} David Gisch and Jason M. Ribando: Apollonius’ Problem: A Study of Solutions and Their Connections. (pdf) III. The Epstein Soulution. American Journal of Undergraduate Research, 29. Februar 2004, S. 20, archiviert vom Original (nicht mehr online verfügbar) am 15. April 2008; abgerufen am 18. Dezember 2023 (englisch).  Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/www.ajur.uni.edu 
8. ↑ David Eppstein: Tangent Spheres and Triangle Centers. (pdf) The Mathematical Assosiation of Amerika, Januar 2001, S. 63–66, abgerufen am 17. Dezember 2023 (englisch). 
9. ↑ H. Lee Price: The Pythagorean Tree: A New Species. (PDF) 2 On Parameters, Angles, and Fibonacci Boxes. arxiv, Cornell University, September 2008, S. 8–9, abgerufen am 8. Februar 2024 (englisch). 
10. ↑ Frank Bernhart, H. Lee Price: Heron’s Formula, Descartes Circles, and Pythagorean Triangles. (PDF) 5 Pythagorean Triangles. arxiv, Cornell University, 1. Januar 2007, S. 9–11, abgerufen am 8. Februar 2024 (englisch).