Mécanique spatiale

La mécanique spatiale, aussi dénommée astrodynamique, est, dans le domaine de l'astronomie et de l'astronautique, la science qui a trait à l'étude des mouvements. C'est une branche particulière de la mécanique céleste qui a notamment pour but de prévoir les trajectoires des objets spatiaux tels que les fusées ou les engins spatiaux y compris les manœuvres orbitales, les changements de plan d'orbite et les transferts interplanétaires.

Lois fondamentales

Lois de Kepler

Les premières lois de mécanique spatiale furent découvertes expérimentalement par l'observation du mouvement des planètes par Kepler au début du XVII^e siècle. Elles constituent les lois du mouvement képlérien. Rappelons ici les principaux résultats :

• Première loi (1609) : les orbites des planètes sont des ellipses planes dont le Soleil occupe l'un des foyers.
• Seconde loi (1609) : loi des aires : des aires égales sont balayées par le rayon vecteur joignant le Soleil à la planète en des intervalles de temps égaux.
• Troisième loi (1619) : le rapport entre le cube du demi-grand axe ${\displaystyle a}$ et le carré de la période ${\displaystyle T}$ de révolution de la planète autour du Soleil est indépendant de la planète :
  ${\displaystyle {\frac {a^{3}}{T^{2}}}={\text{cte}}}$
  Elle peut aussi s'écrire mathématiquement :
  ${\displaystyle T=2\pi {\sqrt {\frac {a^{3}}{\mu }}}}$
  où ${\displaystyle T}$ est la période de l'orbite, ${\displaystyle a}$ son demi-grand axe et ${\displaystyle \mu =GM_{S}}$, avec ${\displaystyle G}$ constante de gravitation universelle et ${\displaystyle M_{S}}$ la masse du Soleil.

Ces lois sont encore utilisées avec une bonne approximation dans la plupart des calculs simples de mouvement orbitaux. Il s'agit du type de mouvement orbital de référence, et on calcule notamment des mouvements réalistes comme perturbations faibles d'un mouvement képlérien.

Mouvement à force centrale

Le mouvement képlérien est un mouvement à force centrale. Ceci implique notamment une loi de conservation de l'énergie qui s'écrit dans le cas de l'ellipse :

${\displaystyle {\frac {V^{2}}{2}}-{\frac {\mu }{r}}=-{\frac {\mu }{2a}}}$

${\displaystyle V}$ est la vitesse du corps sur son orbite, ${\displaystyle r}$ la distance entre le corps et le centre attracteur. Les autres notations sont identiques.

Paramètres orbitaux

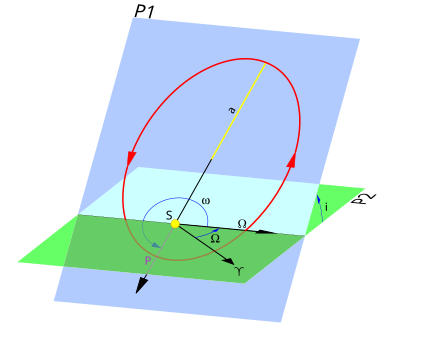
Plutôt que de décrire le mouvement d'un objet spatial par des coordonnées cartésiennes classiques, on va utiliser le fait que le mouvement se déroule sur une ellipse dans l'espace. On peut ainsi remplacer le jeu de 6 coordonnées cartésiennes classique ${\displaystyle (x,y,z,{\dot {x}},{\dot {y}},{\dot {z}})}$ par un jeu de 6 nombres appelées paramètres orbitaux :

• ${\displaystyle a}$ le demi-grand axe de l'orbite
• ${\displaystyle e}$ l'excentricité de l'orbite
• ${\displaystyle i}$ l'inclinaison de l'orbite
• ${\displaystyle \Omega }$ la longitude du nœud ascendant
• ${\displaystyle \omega }$ l'argument du périastre
  (périhélie dans le cas du Soleil, périgée dans le cas de la Terre)
• Un nombre permettant de repérer la position sur l'orbite, au choix :
  • ${\displaystyle \nu }$ anomalie vraie, ou
  • ${\displaystyle E}$ anomalie excentrique, ou
  • ${\displaystyle M}$ anomalie moyenne.

Il existe des formules explicites permettant de passer entre ces 2 jeux de coordonnées (référence à venir).

Les paramètres orbitaux des objets (satellites et débris spatiaux) en orbite terrestre sont suivis en permanence et publiés dans un format standard (voir TLE, Two-Line Elements).

Repères en mécanique spatiale

Pour décrire une orbite à l'aide des paramètres orbitaux, le référentiel galiléen choisi sera géocentrique ; ses axes sont l’axe Nord-Sud de la Terre, fixe en première approximation, l’axe vernal (l’intersection entre le plan équatorial et le plan de l’écliptique à un instant donné) et le dernier tel que les trois forment un repère orthonormé direct.

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue ! Comment faire ?

Mouvement képlérien perturbé

Les calculs standards en mécanique spatiale se réalisent dans un cadre képlérien, où en particulier, on suppose que la seule force agissant sur le véhicule est l'attraction terrestre, et que la Terre est sphérique et homogène. Ces deux hypothèses sont fausses en réalité ; l'expérience montre néanmoins que les accélérations causées par les forces autres que l'attraction centrale sont faibles devant l'accélération képlérienne. C'est pourquoi on considère que les autres forces sont des perturbations du mouvement.

Forces de perturbations

Forces gravitationnelles

Ces forces ne dépendent que de la répartition des masses autour du satellite, et dérivent d'un potentiel de position. Notons ${\displaystyle U}$ ce potentiel.

Potentiel terrestre

Dans le cas képlérien, la Terre est sphérique, et le potentiel terrestre se calcule simplement, et vaut ${\displaystyle {\tfrac {\mu }{r}}}$. Dans le cas réel, le volume d'intégration est beaucoup plus complexe. Pour avoir une forme exploitable, on écrit ce potentiel sous la forme d'harmoniques sphériques, et on obtient :

${\displaystyle U={\frac {\mu }{r}}+{\frac {\mu }{r}}\sum _{n=1}^{\infty }\left({\frac {r_{eq}}{r}}\right)^{n}\left\lbrack -J_{n}P_{n}(\sin \phi )+\sum _{m=1}^{n}\lbrace C_{nm}\cos(m\lambda )+S_{nm}\sin(m\lambda )\rbrace P_{mn}\sin(\phi )\right\rbrack }$

Dans cette expression, ${\displaystyle r_{eq}}$ est le rayon équatorial terrestre, ${\displaystyle J_{n}}$ est une constante inertielle de la Terre appelée harmonique zonal d'ordre n, ${\displaystyle C_{nm}}$ et ${\displaystyle S_{nm}}$ sont également des constantes d'inertie appelées harmoniques tesseraux, ${\displaystyle P_{n}}$ est le polynôme de Legendre d'ordre n, ${\displaystyle P_{nm}}$ la fonction de Legendre propre associée. ${\displaystyle r}$, ${\displaystyle \lambda }$ et ${\displaystyle \phi }$ sont le rayon-vecteur, la longitude et la latitude géocentrique du point où l'on calcule le potentiel.

Le premier terme de ce développement, ${\displaystyle J_{2}}$, traduit l'aplatissement aux pôles. Ce terme a une intensité relative de ${\displaystyle 10^{-3}}$ par rapport au potentiel képlérien, tandis que les termes suivants sont en ${\displaystyle 10^{-6}}$.

Attraction due à la Lune ou au Soleil

En prenant un repère dans lequel le véhicule a pour coordonnées ${\displaystyle (x,y,z)}$ et le nouveau corps attracteur, Lune ou Soleil, ${\displaystyle (x',y',z')}$, alors le potentiel supplémentaire dû à ce corps s'écrit :

${\displaystyle U_{p}=\mu _{p}\left({\frac {1}{\Delta }}-{\frac {xx'+yy'+zz'}{r_{p}^{3}}}\right)}$

avec :

${\displaystyle \Delta ^{2}=r_{p}^{2}+r^{2}-2(xx'+yy'+zz')}$

L'ordre de grandeur rapporté au potentiel képlérien est de ${\displaystyle 10^{-8}}$ dans le cas du Soleil et de ${\displaystyle 10^{-7}}$ pour la Lune.

Forces non-gravitationnelles

Ces forces, contrairement aux précédentes, ne dérivent pas d'un potentiel. On va donc cette fois calculer les accélérations induites par ces forces.

Frottement atmosphérique

La force du frottement atmosphérique est due à l'interaction entre l'atmosphère et le véhicule. Vu les hautes vitesses des engins satellisés, malgré la faible densité de l'atmosphère à ces altitudes, on ne peut négliger cette force qu'à partir de 1 500 km d'altitude.

La force créée le long de l'axe de la vitesse de l'engin, qui sera donc opposée à cette vitesse, s'écrit :

${\displaystyle \gamma _{f}={\frac {1}{2}}\rho SV_{r}^{2}{\frac {C_{x}}{m}}}$

Dans cette relation, ${\displaystyle \rho }$ est la densité de l'atmosphère, ${\displaystyle S}$ une surface de référence, ${\displaystyle V_{r}}$ la vitesse du véhicule par rapport à l'atmosphère, ${\displaystyle C_{x}}$ le coefficient de traînée du véhicule et ${\displaystyle m}$ sa masse.

Il existe également des forces de nature similaire selon les autres axes de coordonnées (forces de portance par exemple) mais leurs effets sont en général plus faibles. Selon l'altitude, cette force de frottement a des intensités rapportées à celle du potentiel képlérien de ${\displaystyle 10^{-4}}$ à ${\displaystyle 10^{-9}}$.

Pression de radiation solaire

Cette force est due à l'interaction des photons avec le véhicule. L'accélération due à la pression de radiation directe venant du Soleil peut s'écrire :

${\displaystyle {\vec {\gamma _{p}}}=\epsilon SP_{0}{\frac {C_{p}}{m}}{\vec {u}}}$

${\displaystyle \epsilon }$ est un coefficient valant 1 si le satellite est éclairé et 0 sinon, ${\displaystyle S}$ est une surface de référence, ${\displaystyle P_{0}}$ la pression de radiation solaire directe par unité de surface, valant en moyenne 4,63 × 10⁻⁶ N m⁻², ${\displaystyle C_{p}}$ le coefficient de réflexivité, de l'ordre de ${\displaystyle 1,5}$,et ${\displaystyle {\vec {u}}}$ le vecteur unitaire de la direction Soleil-véhicule.

Équations du mouvement perturbé

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue ! Comment faire ?

Équations de Lagrange

Équations de Gauss

Manœuvres orbitales

Le principe général des manœuvres est de modifier un ou plusieurs paramètres orbitaux à l'aide des moyens de propulsion de l'objet spatial considéré.

Force de poussée et variation de masse de l'engin

Dans le cas d'une propulsion avec moteur à ergol, la force de poussée peut s'écrire :

${\displaystyle F=-{\dot {m}}g_{0}I_{sp}}$

${\displaystyle {\dot {m}}}$ est le débit de matière entrant, ${\displaystyle g_{0}}$ la constante de gravitation, et ${\displaystyle I_{sp}}$ l'impulsion spécifique.

Fréquemment, lors des manœuvres, cette poussée s'effectue pendant un temps négligeable devant la période de l'orbite. On peut alors faire l'hypothèse de poussée impulsionnelle : on considère alors que cette poussée se produit de façon instantanée. Cette hypothèse permet d'utiliser l'équation de Tsiolkowski pour approximer la variation de masse d'ergol pendant la manœuvre :

${\displaystyle \Delta m=m_{0}(1-e^{\frac {|\Delta V|}{g_{0}I_{sp}}})}$

Dans ce cas ${\displaystyle \Delta V}$ est la variation du module de la vitesse pendant la manœuvre et ${\displaystyle m_{0}}$ la masse initiale d'ergol.

Modification de la forme de l'orbite

On cherche à modifier les paramètres de forme ${\displaystyle a}$ et ${\displaystyle e}$, de façon à minimiser l'ergol consommé. On montre que pour un ${\displaystyle \Delta a}$ donné, ${\displaystyle \Delta V}$ est minimum si la poussée est colinéaire à la vitesse et la vitesse est maximale.

On réalise donc les manœuvres au périastre, qui remplit les 2 conditions. Les manœuvres optimales de modification de la forme de l'orbite consistent alors à modifier l'apoastre.

Un exemple d'orbite de transfert utilisant cette manœuvre optimale est l'orbite de Hohmann.

Modification du plan de l'orbite

On cherche cette fois à modifier les paramètres ${\displaystyle i}$ et ${\displaystyle \Omega }$. Si l'on souhaite modifier ${\displaystyle i}$ uniquement, il s'agit d'effectuer la manœuvre au niveau du nœud ascendant ou descendant, pour faire tourner l'orbite autour de cette ligne. Si on veut passer de l'inclinaison ${\displaystyle i_{1}}$ à l'inclinaison ${\displaystyle i_{2}}$, on montre que la variation de vitesse nécessaire s'écrit :

${\displaystyle \Delta V=2V_{0}\sin \left({\frac {i_{2}-i_{1}}{2}}\right)}$

${\displaystyle V_{0}}$ est alors la vitesse au nœud de manœuvre.

Les modifications de ${\displaystyle \Omega }$ sont quant à elles complexes et coûteuses en ergols.

Références

• Droit français : arrêté du 20 février 1995 relatif à la terminologie des sciences et techniques spatiales.
• B.Escudier, J-Y Pouillard, Mécanique spatiale, Toulouse, ENSAE Toulouse, 1997 (réimpr. 1996, 1997), 111 p. (ISBN 2-84088-028-8)
  Polycopié de l'ISAE sur la mécanique spatiale.

• O.Zarrouati, Trajectoires spatiales, Toulouse, CNES - Cépadues Editions

• M-N.Sanz, A-E.Badel, F.Clausset, Physique : Tout-en-un 1^re année, Paris, Dunod - J'intègre, 2002-2003, 725 p. (ISBN 978-2-10-007950-6 et 2-10-007950-6)

Voir aussi

Articles connexes

• Portail de l’astronautique
• Portail de la physique
• Portail de l’astronomie