Involuta
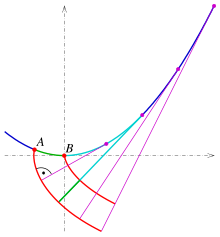
In matematica, date due curve e , si dice che è involuta (o evolvente) di , o che è evoluta di , se appartiene allo spazio generato dal vettore tangente di per ogni punto del dominio e se gli spazi 1-dimensionali generati dai vettori tangenti di e siano ortogonali in tutto il loro dominio. Per esempio la curva dei centri dei cerchi osculatori di è un’evoluta di .
Geometricamente, un'involuta, è un particolare tipo di curva che dipende da un'altra forma o curva. L'involuta di una curva è il luogo dei punti toccati dall'estremo di un pezzo di corda tesa mentre viene avvolta (o srotolata, in modo geometricamente equivalente) attorno alla curva data.[1]
Le involute appartengono alla famiglia di curve chiamate roulette.
L'evoluta di un'involuta è quindi la curva originaria.
Le nozioni di involuta e di evoluta di una curva furono introdotte da Christiaan Huygens nel suo lavoro intitolato Horologium oscillatorium sive de motu pendulorum ad horologia aptato dimostrationes geometricae (1673).[2]
Involuta di una curva parametrizzata
Sia una curva regolare sul piano con curvatura mai nulla e , allora la curva con la rappresentazione parametrica
è un'involuta della curva data.
Dimostrazione
Aggiungendo di un numero arbitrario ma fisso all'integrale risulta in un'involuta corrispondente a una corda estesa di (come una palla di filo si lana, avente una certa lunghezza di filo già appeso prima che sia svolto). Quindi, l'involuta può variare di una costante e/o aggiungendo un numero all'integrale (vedi involuta di una parabola semicubica).
Se si ottiene
Proprietà delle involute

Per ricavare le proprietà di una curva regolare è vantaggioso utilizzare la lunghezza dell'arco come il parametro della curva assegnata, che porta alle seguenti semplificazioni: e , con la curvatura e l'unità normale. Si ottiene per l'involuta:
- e
oltre al seguente risultato:
- nel punto l'involuta non è regolare (perché ).
Da segue che:
- La normale dell'involuta al punto è la tangente della curva data nel punto .
- Le involute sono curve parallele, poiché e poiché è il vettore unitario normale a .
Esempi
Involuta di una circonferenza

Per una circonferenza con rappresentazione parametrica , si ha . Quindi e la lunghezza del percorso è .
Calcolando l'equazione sopra indicata dell'involuta, si ottiene
per l'equazione parametrica dell'involuta della circonferenza.
La lunghezza dell'arco per e dell'involuta è
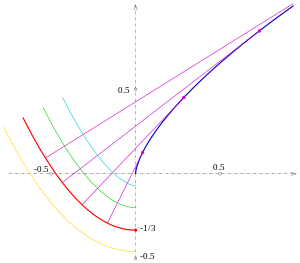
Involute di una parabola semicubica
L'equazione parametrica , l'equazione dell'involuta è quindi
Eliminando si ottiene dimostrando che questa involuta è una parabola.
Le altre involute sono quindi curve parallele di una parabola e non sono parabole, poiché sono curve di grado sei.
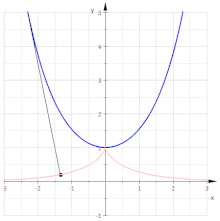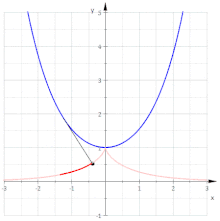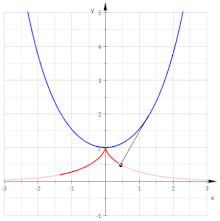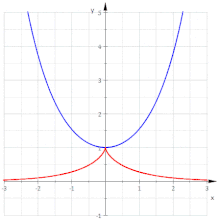
Involute di una catenaria
Per la catenaria , il vettore tangente è , e come la sua lunghezza è . Quindi la lunghezza dell'arco dal punto (0, 1) è
Quindi l'involuta a partire da è parametrizzata da
ed è quindi una trattrice.
Le altre involute non sono trattrici, poiché sono curve parallele di una trattrice.

Involute di una cicloide
La rappresentazione parametrica descrive una cicloide. A partire dal , si ottiene (dopo aver usato alcune formule trigonometriche)
e
Quindi le equazioni dell'involuta corrispondente sono
che descrivono la cicloide rossa spostata del diagramma. Quindi le involute della cicloide sono curve parallele della cicloide
Le curve parallele di una cicloide non sono cicloidi.
Involute ed evolute
L'evoluta di una data curva è costituita dai centri di curvatura di . Tra involute ed evolute vale la seguente relazione:[3][4]
- Una curva è l'evoluta di una qualsiasi delle sue evolventi (involute).
- Involuta ed evoluta
-
 Una trattrice (in rosso) come un'involuta di una catenaria
Una trattrice (in rosso) come un'involuta di una catenaria -
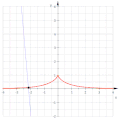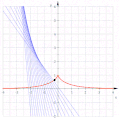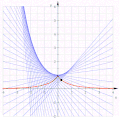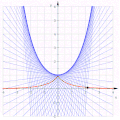 L'evoluta di una trattrice è una catenaria
L'evoluta di una trattrice è una catenaria
Applicazioni
L'involuta ha alcune proprietà che lo rendono estremamente importante per l'industria degli ingranaggi: se due ingranaggi a maglie incrociate hanno denti con la forma del profilo di involute (piuttosto che, ad esempio, una forma triangolare tradizionale), formano un sistema di ingranaggi a spirale. Le loro velocità di rotazione relative sono costanti mentre i denti sono impegnati. Gli ingranaggi inoltre entrano sempre in contatto lungo un'unica linea di forza costante. Con denti di altre forme, le velocità e le forze relative aumentano e diminuiscono quando i denti successivi si impegnano, provocando vibrazioni, rumore e usura eccessiva. Per questo motivo, quasi tutti i moderni ingranaggi hanno la forma a evolvente.[5]

Note
- ^ J.W. Rutter, Geometry of Curves, CRC Press, 2000, pp. 204, ISBN 9781584881667.
- ^ John McCleary, Geometry from a Differentiable Viewpoint, Cambridge University Press, 2013, pp. 89, ISBN 9780521116077.
- ^ K. Burg, H. Haf, F. Wille, A. Meister: Vektoranalysis: Höhere Mathematik für Ingenieure, Naturwissenschaftler und ..., Springer-Verlag, 2012,ISBN 3834883468, S. 30.
- ^ R. Courant:Vorlesungen über Differential- und Integralrechnung, 1. Band, Springer-Verlag, 1955, S. 267.
- ^ V. G. A. Goss (2013) "Application of analytical geometry to the shape of gear teeth", Resonance 18(9): 817 to 31 Springerlink (subscription required).
Voci correlate
- Evoluta
- Compressore Scroll
- Ingranaggio a spirale
- Rulletta
Altri progetti
Altri progetti
- Wikimedia Commons
 Wikimedia Commons contiene immagini o altri file su evolvente
Wikimedia Commons contiene immagini o altri file su evolvente
Collegamenti esterni
- Involuta in MathWorld


![{\displaystyle {\vec {c}}(t),\;t\in [t_{1},t_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b014b9d8601fa970d2eaa1f8132f2f34ec432233)





























































