Metodo delle maglie

Questa voce o sezione sull'argomento fisica non cita le fonti necessarie o quelle presenti sono insufficienti.

Si definisce metodo delle maglie o più propriamente metodo delle correnti di anello oppure metodo delle correnti fittizie il procedimento risolutivo per circuiti di bipoli, sia in regime stazionario che sinusoidale, per determinare tutte le correnti di maglia, e di lato poi.

Avendo a mente la seconda delle leggi di Kirchhoff scomponiamo il circuito in maglie ed assegniamo ad ognuna una corrente arbitraria fissando un riferimento comune, in quanto è opportuno che tutte le correnti abbiano lo stesso verso.

In tal modo possiamo determinare le correnti di lato per differenza delle due correnti di maglia che hanno il lato in comune.

Primo caso

Si considerano adesso le reti lineari in regime stazionario in cui siano presenti solo generatori di tensione.

Ricordando la LKT:

\sum _{maglia}\pm u(t)=0

questa può essere riscritta considerando le tensioni dei resistori come $U_{h}=R_{h}I_{h}$ e le tensioni dei generatori di tensione come $U_{h}=E_{h}$ ottenendo così:

\sum _{maglia}R_{h}I_{h}=\sum _{maglia}E_{h}

esprimendo le correnti di lato come differenza delle correnti di maglia $R_{h}I_{h}=R_{h}(I_{m_{i}}-I_{m_{j}})$ , scrivendo questa equazione per ogni maglia del circuito otteniamo un sistema di m equazioni con m incognite pari alle maglie del sistema:

{\begin{cases}\sum R_{m_{1}}I_{m_{1}}-\sum _{r=2}^{m}R_{1_{r}}I_{1_{r}}=\sum E_{m_{1}}\\\sum R_{m_{2}}I_{m_{2}}-\sum _{r=1,r\neq 2}^{m}R_{2_{r}}I_{2_{r}}=\sum E_{m_{2}}\\................\\\sum R_{m_{m}}I_{m_{m}}-\sum _{r=1}^{m-1}R_{m_{r}}I_{m_{r}}=\sum E_{m_{m}}\\\end{cases}}

dove:

$I_{m_{1}},...I_{m_{m}}$ sono le correnti di maglia
$\sum R_{m_{1}},...\sum R_{m_{m}}$ è la somma di tutte le resistenze presenti nella maglia e quindi percorse dalla corrente di maglia
$R_{1_{r}},...R_{m_{r}}$ sono le resistenze in comune tra la maglia considerata e quelle contigue percorse dalle relative correnti
$\sum E_{m_{1}},...\sum E_{m_{m}}$ è la somma algebrica dei contributi dei generatori presenti nella maglia.

Il sistema costituisce il metodo delle maglie: una volta risolto il sistema abbiamo le correnti di maglia dalle quali possiamo prima ricavare le correnti di lato e poi le tensioni mediante le equazioni di bipolo.

Esempio primo caso

scriviamo il sistema di 3 equazioni in tre incognite:

\left\{{\begin{matrix}(R_{1}+R_{6}+R_{7}+R_{8})I_{m_{A}}&-R_{6}I_{m_{B}}&-R_{7}I_{m_{C}}&=&\Delta V\\-R_{6}I_{m_{A}}&+(R_{6}+R_{2}+R_{4})I_{m_{B}}&-R_{4}I_{m_{C}}&=&0\\-R_{7}I_{m_{A}}&-R_{4}I_{m_{B}}&+(R_{7}+R_{3}+R_{4})I_{m_{C}}&=&0\end{matrix}}\right.

in forma matriciale

{\begin{bmatrix}(R_{1}+R_{6}+R_{7}+R_{8})&-R_{6}&-R_{7}\\-R_{6}&(R_{6}+R_{2}+R_{4})&-R_{4}\\-R_{7}&-R_{4}&(R_{7}+R_{3}+R_{4})\end{bmatrix}}.{\begin{bmatrix}I_{m_{A}}\\I_{m_{B}}\\I_{m_{C}}\end{bmatrix}}={\begin{bmatrix}\Delta V\\0\\0\end{bmatrix}}

Da cui si calcola il vettore delle correnti di maglia; volendo sapere la corrente di lato tra il nodo 2 e nodo 3:

I_{l_{23}}=I_{m_{B}}-I_{m_{C}}

e se volessimo la tensione ai capi:

U_{23}=I_{l_{23}}R_{4}

Caso generale

Si considerano, adesso, le reti lineari in regime stazionario in cui siano presenti sia generatori di tensione che generatori di corrente.

I generatori di correnti possono essere reali o ideali:

nel primo caso si presenta un generatore reale con in parallelo un resistore, quindi considerando i due bipoli insieme si possono trasformare in un generatore di tensione equivalente $E_{eq}=JR$ con in serie lo stesso resistore ritornando al caso noto.
nel caso di un generatore ideale di corrente si trasforma sempre in un generatore equivalente di tensione ma questa risulterà incognita, così da costituire una nuova incognita del sistema che per essere risolto avrà bisogno di un'ulteriore equazione; questa è costituita dall'equazione delle correnti del generatore che può essere scritta:

\sum I_{m_{i}}=J

così il nostro sistema diverrà:

{\begin{cases}\sum R_{m_{1}}I_{m_{1}}-\sum _{r=2}^{m}R_{1_{r}}I_{1_{r}}=\sum E_{m_{1}}+\sum \Delta U_{m_{1}}\\\sum R_{m_{2}}I_{m_{2}}-\sum _{r=1,r\neq 2}^{m}R_{2_{r}}I_{2_{r}}=\sum E_{m_{2}}+\sum \Delta U_{m_{1}}\\................\\\sum R_{m_{m}}I_{m_{m}}-\sum _{r=1}^{m-1}R_{m_{r}}I_{m_{r}}=\sum E_{m_{m}}+\sum \Delta U_{m_{1}}\\\sum I_{m_{1}}=J_{a}\\......\\\sum I_{m_{m}}=J_{z}\end{cases}}

ottenendo così ancora un sistema $(m+n)\times (m+n)$ risolvibile, con m(maglie)+n(generatori di corrente ideali) equazioni e m+n incognite: ancora una volta risolto il sistema abbiamo le correnti di maglia dalle quali le correnti di lato e poi le tensioni mediante le equazioni di bipolo.

Esempio caso generale

Considerando il circuito sopra indicato abbiamo 4 maglie e 2 generatori di corrente, quindi otterremo un sistema 6x6:

\left\{{\begin{matrix}(R_{1}+R_{4})I_{m_{1}}&-R_{4}I_{m_{2}}&&&=&E_{1}\\-R_{4}I_{m_{1}}&+(R_{3}+R_{4})I_{m_{2}}&-R_{3}I_{m_{3}}&&=&E_{2}\\&-R_{3}I_{m_{2}}&+(R_{2}+R_{3})I_{m_{3}}&-R_{2}I_{m_{4}}&=&\Delta U_{1}\\&&-(R_{2})I_{m_{3}}&+R_{2}I_{m_{4}}&=&\Delta U_{2}\\I_{m_{3}}=J_{1}\\I_{m_{4}}=-J_{2}\end{matrix}}\right.

avendo numerato le correnti di maglia da destra verso sinistra e indicato con $\Delta U_{1}\,,\Delta U_{2}$ le tensione ai capi dei generatori ideali di corrente.

Per rendere il sistema più semplice possiamo sostituire il generatore $J_{2}$ in parallelo con $R_{2}$ con un generatore di tensione equivalente $E_{2J}=R_{2}J_{2}$ :

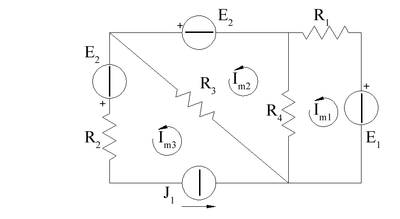
così il sistema sarà un 4x4:

\left\{{\begin{matrix}(R_{1}+R_{4})I_{m_{1}}&-R_{4}I_{m_{2}}&&=&E_{1}\\-R_{4}I_{m_{1}}&+(R_{3}+R_{4})I_{m_{2}}&-R_{3}I_{m_{3}}&=&E_{2}\\&-R_{3}I_{m_{2}}&+(R_{2}+R_{3})I_{m_{3}}&=&\Delta U_{1}+E_{2J}\\I_{m_{3}}=J_{1}\end{matrix}}\right.

che risolvendo e scritto in forma matriciale:

{\begin{bmatrix}(R_{1}+R_{4})&-R_{4}&&\\-R_{4}&(R_{3}+R_{4})&\\&-R_{3}&-1&\end{bmatrix}}.{\begin{bmatrix}I_{m_{1}}\\I_{m_{2}}\\\Delta U_{1}\end{bmatrix}}={\begin{bmatrix}E_{1}\\E_{2}+R_{3}J_{1}\\-(R_{2}+R_{3})J_{1}\end{bmatrix}}

Un altro modo di procedere per semplificare il circuito e abbassare il rango del sistema è introdurre una semplificazione topologica del circuito. In particolare possiamo considerare il lato $l_{12}$ con il generatore di corrente ideale e staccarlo una estremità per volta per connetterlo alternativamente al nodo 3 ottenendo così il seguente circuito:

dove notiamo che il nostro sistema si è scomposto in 2 circuiti connessi in un solo punto (nodo 3).

Per risolvere questo circuito, una volta sostituito il parallelo del generatore $J_{1}$ e la resistenza $R_{3}$ con un generatore reale di tensione $E_{1J}=R_{3}J_{1}$ , otteniamo un sistema con 3 equazioni di cui una indipendente:

sistema 2x2 per descrivere il circuito di destra:

\left\{{\begin{matrix}(R_{1}+R_{4})I_{m_{1}}&-R_{4}I_{m_{2}}&=&E_{1}\\-R_{4}I_{m_{1}}&+(R_{3}+R_{4})I_{m_{2}}&=&E_{2}+E_{1J}\end{matrix}}\right.

mentre il circuito di sinistra è a corrente imposta presentato il parallelo di due generatori di corrente che andranno semplicemente sommati considerando i segni.

È da notare che mediante il metodo dei nodi la soluzione dell'esercizio è ancora più semplice dovendo imporre solo un'equazione che permette di conoscere la tensione ai nodi 2 e 4 tramite il Teorema di Millman.