 関数
関数  のルジャンドル変換
のルジャンドル変換  (ただし
(ただし  )は、
)は、 における
における  の接線の切片に対応している。
の接線の切片に対応している。 ルジャンドル変換(ルジャンドルへんかん、英: Legendre transformation)とは、凸解析において、関数の変数をその微分に変えるために用いられる変換である。このとき実数関数 f(x) は微分可能でなくてもよいが連続関数だとする[1]。
名前はフランスの数学者、アドリアン=マリ・ルジャンドルに因む。ルジャンドル変換は点と線の双対性、つまり凸な関数 y = f (x) は (x, y) の点の集合によって表現できるが、それらの傾きと切片の値で指定される接線の集合によっても等しく充分に表現できることに基いている。
凸関数をルジャンドル変換する際、変換前の関数が保持している情報は、変換後の関数においても完全に保たれる。解析力学においてはこの性質を利用して、ラグランジアンからルジャンドル変換によってハミルトニアンが得られる(⇒#解析力学)。物理学等において他にも広く応用されており、熱力学における熱力学関数間の変換などにも用いられる(⇒#熱力学)。
ルジャンドル変換をより一般化したものはルジャンドル=フェンシェル変換と呼ばれる。
定義
関数 f(x) のルジャンドル変換 f*(p) は次のように定義される:

または

ここで supx および infx は変数 x を動かしたときの上限および下限を表す[注 1]。
また、下に凸な関数に対して等価な、別の定義として以下がある。

at 以下は、「f′(x − 0) ≤ p ≤ f′(x + 0) を満たすような x を、一意でなければどれでもいいから代入せよ」という意味である。
変換される関数 f は x 以外の変数を持っていてもよく、多変数関数に対しては各変数についてルジャンドル変換をすることができる。
性質
その定義から明らかなように、関数 g(x) = px − f(x) の上限が定まる場合のみ、ルジャンドル変換によって新しい関数 f*(p) を与えることができる。
それが定まる場合でも、もととなる関数 f(x) が凸関数でない場合、新たに定義された関数 f*(p) は逆変換してももとの関数 f(x) へは戻らない。したがって応用上は初めから関数 f(x) は凸であると仮定することが多い。
滑らかな関数に対する変換
もとの関数 f(x) の一階の導関数 f'(x) が x について連続であり単調増加する場合、すなわち関数 f(x) が下に凸で滑らかな場合、関数 g(x) = px − f(x) の上限となる x は、g(x) の x の一階の導関数 g'(x) が 0 になる点であるから、ルジャンドル変換は次のように書き直せる。

ここで関数 x*(p) は f(x) の導関数 f'(x) の逆関数である:

これは方程式 f'(x) = p の解である。
また、f もそのルジャンドル変換 f * も2階微分可能なら、両者は逆数の関係にある。すなわち

ただし x と p は p = f′(x) を満たすとする。
逆変換
関数 f(x) のルジャンドル変換 f*(p) に対して再びルジャンドル変換を施した関数を f**(x) とする:

f(x) が下に凸であれば、f**(x) はもとの関数 f(x) に等しい:

つまりルジャンドル変換の逆変換はルジャンドル変換そのものとなる。
簡単な証明として、関数が滑らかな凸関数である場合についてこのことを示す。まず関数 f を 2 回ルジャンドル変換をすると以下のようになる。

p*(x) は d/dp f*(p) の逆関数であり、x*(p) は f'(x) = d/dx f(x) の逆関数なので、

p*(x) は x*(p) の逆関数でもあり、x*(p*(x)) = x が成り立つ。 このことから、f** はもとの関数 f に等しいことが示される。

ヤングの不等式
以下の不等式が成り立つ。この種の不等式はヤングの不等式と呼ばれる。

ルジャンドル変換の定義より、

であるから、f(x) を両辺に足せば上述の不等式が成り立つ。
その他
- f (x) が下(上)に凸なら f *(p) も下(上)に凸。すなわちルジャンドル変換は凸性を保持する。
- f (x) の左微分と右微分が異なる( f (x) が折れ線となる)点は、f *(p) が p に関して1次関数(直線)となる領域に対応する。逆に f (x) が x に関して直線となる領域は f *(p) が折れ線となる点に対応する。これは感覚的には、
 と
と  が対応するとも解釈できる。
が対応するとも解釈できる。 - 象徴的に書けば、以下のように x と p について対称な関係がある。

- f (x) の逆関数 f -1 (x) のルジャンドル変換は以下である(後述のヘルムホルツエネルギーとマシュー関数(英語版)の関係などに応用がある)。

多変数関数
多変数関数に対しては、その一部の変数に関してだけのルジャンドル変換を考えることができる。
2変数関数 f(x, y) を x についてルジャンドル変換した関数を f*(p, y) とする。このとき、変換されない変数 y はスペクテータと呼ばれる。スペクテータ y による偏微分はルジャンドル変換の影響を受けない。すなわち次式が成り立つ:

応用例
熱力学
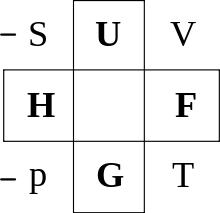 ルジャンドル変換で繋がっている熱力学関数とその変数のまとめ。
ルジャンドル変換で繋がっている熱力学関数とその変数のまとめ。 熱力学では、熱力学関数間の変換、すなわち内部エネルギー U(S, V) をエンタルピー H(S, p)、ヘルムホルツの自由エネルギー F(T, V) に、またそれらからギブスの自由エネルギー G(T, p) に変換する際にルジャンドル変換が用いられる。

ここで、V:体積、p:圧力、S:エントロピー、T:温度である。U が S, V について下に凸であるため、U(S, V), H(S, p), F(T, V), G(T, p) はルジャンドル変換を介して互いに等価である(同じ情報を持つ)。
ただしここではルジャンドル変換は

という定義が用いられる。この定義でも上に述べた性質はほぼ同様に成り立つが、符号や凸性の変化などがある。たとえば逆変換は

に変わるという不便さがある。しかし多変数関数をこの定義で変換した場合、凸性の上下については、変換した変数についてのみ逆転し残りの変数についてはもとのまま保持されるという簡便さがある。
熱力学では導関数の不連続性は相転移として現れる。
解析力学
 解析力学におけるルジャンドル変換にThermodynamic square(英語版)を適用したときのオイラー=ラグランジュ方程式。
解析力学におけるルジャンドル変換にThermodynamic square(英語版)を適用したときのオイラー=ラグランジュ方程式。  Thermodynamic square(英語版)を適用したときの正準方程式。
Thermodynamic square(英語版)を適用したときの正準方程式。 解析力学では、ラグランジアン L をハミルトニアン H に変換する際に、ルジャンドル変換が用いられる。座標を q としたときに正準運動量を p = ∂L/∂·q として、ハミルトニアンは

と定義される。これによって、L(q, ·q) から H(q, p) になる。 実際これは以下の関係を満たす。

このハミルトニアンとオイラー=ラグランジュ方程式あるいは最小作用の原理を組み合わせることで正準方程式が導かれる。 ハミルトニアンの全微分は、

と書けるが、一方でハミルトニアンの定義より、

となるので、ハミルトニアンの偏微分は以下の関係を満たす。この内、正準変数 p, q の偏微分に関する式をまとめて正準方程式 (canonical equations) と呼ぶ。

逆にハミルトニアンからラグランジアンを得る場合には、関数 L を以下のように定義し、

変数 p に対する偏微分が 0 になるようにする。すなわち、

結局このとき変数 ·q はハミルトニアンの運動量微分に等しくなる。
多変数の場合には、ラグランジアンのすべての一般化速度についてルジャンドル変換を施したものがハミルトニアンと呼ばれる。また部分的にルジャンドル変換をしたものはラウシアン(英語版) (Routhian) と呼ばれる。
正準変換
具体例
滑らかな関数の例
最も簡単な例として特異性のない関数を挙げる。定数 s > 1 に対して

とする。この関数 f は下に凸かつ十分滑らかである。関数 f のルジャンドル変換 f* は

となる。ただし t は 1/s + 1/t = 1 を満たす定数である。この例では f(x) と f *(p) は対称な形となる。特に s = t = 2 の場合、f(x) = x2/2 はルジャンドル変換で形を変えない。
導関数に定数となる領域がある例
f (x) がある区間で1次関数(直線)となる例を挙げる。

導関数 f'(x) が全領域で連続、かつ Template:Math2= で定数 f'(x) = 1 であることに注意する。この関数のルジャンドル変換は p = 1 で折れ線となり、

となる。
斉次関数
f(x) が k 次の斉次関数であるなら、そのルジャンドル変換は

である。特に k = 1 のとき、f(x) のルジャンドル変換は 0 となる。
注釈
- ^ より初等的な最大値や最小値を用いて

または 
としている文献もある。ただしこの場合最大値や最小値には無限大も含むこととする。
出典
- ^ 谷村省吾,. “ルジャンドル変換、物質情報学 1(解析力学)講義ノート 6” (pdf). 2022年8月27日閲覧。
参考文献
- 田崎, 晴明『熱力学 現代的な視点から』(初版)培風館〈新物理学シリーズ 32〉、2000年4月12日、302頁。ISBN 9784563024321。 付録 H. Legendre 変換、pp.270-278.
- 須藤, 靖『解析力学・量子論』(第 2 版)東京大学出版会、2010年8月20日、274頁。ISBN 9784130626101。 5.2 ルジャンドル変換、pp.45-47.
- 清水, 明『熱力学の基礎』東京大学出版会、2007年、221-254頁。ISBN 978-4-13-062609-5。
- 菅野, 礼司『微分形式による特殊相対論』丸善、1996年、152頁。ISBN 4-621-04262-9。
- 二間瀬, 敏史、綿村, 哲『解析力学と相対論』朝倉書店、2010年。ISBN 978-4-254-13772-9。
関連項目
外部リンク

















































