余核
 | 「Coker (数学)」はこの項目へ転送されています。その他の用法については「en:Coker (disambiguation)」をご覧ください。 |
数学において、ベクトル空間の線型写像 f : X → Y の余核 (よかく、cokernel) は f の終域 の f の像による商空間 Y/im(f) である。余核の次元は f の余次元 (corank) と呼ばれる。
余核は圏論の核の双対であるので、その名前がついている。核は定義域の部分対象であるのに対し(それは定義域に写す)、余核は終域の商対象である(それは終域から写す)。
直感的には、解きたい方程式 f(x) = y が与えられると、余核は方程式が解を持つために y が満たさなければならない制約 - 解の障害物 - を測り、一方核は解の自由さの度合を、存在すれば、測る。これは下で直感で詳述される。
より一般に、ある圏において射 f : X → Y (例えば群の間の準同型やヒルベルト空間の間の有界線型作用素)の余核は対象 Q と射 q : Y → Q であって合成 q f が圏のゼロ射であり、さらに、q はこの性質に関して普遍的であるようなものである。しばしば写像 q は省略され Q 自身が f の余核と呼ばれる。
アーベル群、ベクトル空間、加群といった抽象代数学の多くの状況において、準同型 f : X → Y の余核は Y の f の像による商である。ヒルベルト空間の間の有界線型作用素のような位相的な設定においては、典型的には商にいく前に像の閉包をとらなければならない。
正式な定義
圏論の一般的な枠組みで余核を定義できる。定義が意味を持つには問題の圏がゼロ射をもたなければならない。射 f : X → Y の余核 (cokernel) は f とゼロ射 0XY : X → Y のコイコライザとして定義される。
明示的には、これは次を意味する。f : X → Y の余核は射 q : Y → Q をともなった対象 Q であって図式
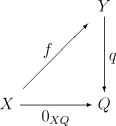
が可換なものである。さらに射 q はこの図式に対して普遍的でなければならない、つまり任意の他のそのような q′: Y → Q′ は q を一意的な射 u : Q → Q′ と合成することによって得られる:
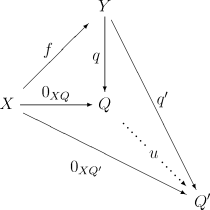
すべての普遍的な構成がそうであるが、余核は、存在すれば、一意的な同型を除いて一意的である、あるいはより正確には: q : Y → Q と q‘ : Y → Q‘ が f : X → Y の2つの余核であれば、一意的な同型 u : Q → Q‘ が存在して q‘ = u q となる。
すべてのコイコライザのように、余核 q : Y → Q はエピ射である必要がある。逆に、エピ射はある射の余核であれば正規(英語版) (normal) (あるいは conormal)と呼ばれる。圏はすべてのエピ射が正規であるときに conormal と呼ばれる(例えば群の圏は conormal である)。
例
群の圏において、群準同型 f : G → H の余核は H の f の像の正規閉包(英語版)による商である。アーベル群の場合、すべての部分群は正規なので、余核は単に f の像を法とした H である:
- coker(f) = H / im(f).
特別な場合
前加法圏において、射を足したり引いたりすることは意味がある。そのような圏において、2つの射 f と g のコイコライザは(存在すれば)それらの差の余核にすぎない:
- .
アーベル圏(前加法圏の特別な種類)において、射 f の像と余像は
によって与えられる。
とくに、すべてのアーベル圏は正規(また conormal)である。つまり、すべてのモノ射 m はある射の核として書ける。具体的には、m はそれ自身の余核の核である:
直感
余核は方程式が満たさなければならない制約の空間として、障害物の空間として、考えることができる。ちょうど核が解の空間であるように。
フォーマルには、核と余核を完全列によって結びつけることができる
これらは次のように解釈できる:解くべき線型方程式 T(v)=w が与えられると、
- 核は斉次方程式 T(v)=0 の解の空間であり、存在すれば、その次元は解の 自由さの度合い の数である。
- 余核は方程式が解を持つならば満たされなければならない 制約 の空間であり、その次元は方程式が解を持つために満たされなければならない制約の数である。
商空間 W/T(V) の次元は単に空間の次元から像の次元を引いたものだから、余核の次元と像の次元(階数)を足すと終域の空間の次元になる。
簡単な例として、T(x,y) = (0,y) で与えられる写像 T: R2 → R2 を考えよう。このとき方程式 T(x,y)=(a,b) が解をもつためには、a=0 でなければならず(1つの制約)、その場合解空間は (x,b) である、あるいは同じことだが、(0,b)+(x,0) である(1 次の自由性)。核は部分空間 (x,0) < V として表現できる: x の値は解の自由さである – 一方余核は実数値写像 W: (a,b) → (a) を通して表現できる: ベクトル (a,b) が与えられると、a の値は解があるための障害物である。
付け加えると、核が単射を「検知する」のと同じように、余核は全射を「検知する」ものとして考えることができる。写像が単射であることと核が自明であることは同値であり、写像が全射であることとその余核が自明であること、あるいは言い換えると、W=im(T) であることは同値である。
参考文献
- Saunders Mac Lane: Categories for the Working Mathematician, Second Edition, 1998.
- Cokernels - page 64











