応力集中

FEMによる応力分布の計算例
赤い部分が応力集中部（高効力部）

応力集中(おうりょくしゅうちゅう、英: stress concentration)とは、物体の形状変化部で局所的に応力が増大する現象である[1]。機械・構造物の疲労破壊や脆性破壊では、この応力集中を起こす部分が破壊の起点となることが多い。

概要

孔が存在する場合の応力線イメージ図

物体に力が負荷されると、物体内部に応力が発生する。一般に、内部の応力の分布は一様ではなく、力の負荷の仕方や物体の形状によって、応力は場所ごとに変化する。特に、孔や溝、段といった一様な形状が変化する部分では応力分布が乱れ、形状変化部の前後に比べて局所的に応力が増大する。このような現象を応力集中と呼び、応力集中を起こす箇所を応力集中部あるいは切欠きと呼ぶ。

以下に代表的な応力集中が問題になる事例を示す。

  • 物体の外形が変化する場合（例：段や溝のような局所的なものから、外板の形状変化部のような骨組みの変化まで）
  • 物体に空洞が存在する場合（例：貫通穴や材料中の空洞欠陥）
  • 集中荷重を受ける場合（例：荷重を受ける範囲が十分に小さいと見なせる場合）
  • 別の物体の接触（例：ヘルツの接触応力）
  • 材料の弾性率が異なる物質が介在する場合（例：金属材料に含まれる非金属介在物）

応力集中がどの程度起こるかは、弾性力学、塑性力学といった個体力学理論による応力分布の解析により解明される。しかし、応力分布の厳密解が判明している問題は限られており、特に3次元問題の解析は2次元問題よりも非常に難しく、厳密解が得られる問題は非常に限られている[2]。そのため、実際の複雑な形状の応力分布を計算する方法としては、有限要素法(FEM)による数値解析が行われている。また、実物で応力分布を計測する方法としては、光弾性応力測定、熱弾性応力測定、ひずみゲージによる応力測定がある。

応力集中部あるいは切欠きは応力が高まることから破壊の起点となり易い。疲労破壊では切欠きから発生したき裂が進展して破壊に至ることが多い。切欠きが存在する場合は、存在しない場合よりも疲労強度が低くなり、このような効果を切欠き効果と呼ぶ。脆性破壊においても、切欠きの存在により脆性破壊が起き易くなる。鉄鋼のような延性材料でも切欠きの存在により脆性的な破壊を起こすことがあり、このような現象を切欠脆性と呼ぶ[3]。

応力集中係数

引張を受けるR付段を持つ丸棒の応力集中係数のグラフ
公称応力は直径が小さい部分での断面積で定義されている。

応力集中の度合いを表すために、応力集中による最大応力を基準となる応力で除した応力集中係数(stress concentration factor)を用いる。

K t = σ m a x σ n {\displaystyle K_{t}={\frac {\sigma _{max}}{\sigma _{n}}}}
ここで
Kt：応力集中係数
σmax：応力集中部の最大応力
σn：公称応力

応力集中係数の他に形状係数(shape factor)とも呼ぶ[4]。記号としては K t {\displaystyle K_{t}} や α {\displaystyle \alpha } が用いられる。

公称応力は応力集中係数を定義するための基準の応力で任意に定義されるものである。公称応力の取り方としては大きく3つの取り方がある[4]。

  • 穴などの応力集中要素がある場合、これらの要素により母体の断面そのものが減少し、応力分布の乱れによる応力集中とは別に正味断面積の平均応力が高まるが、この平均応力で公称応力を定義する場合。
  • 応力集中要素による減少断面積を使わずに定義する公称応力。応力集中部手前の一様形状における遠方応力を使用する場合。
  • 応力集中要素による最大応力を含む断面で定義するが、断面積の計算する際には応力集中要素は存在しない(切欠きが埋まっている)場合の断面積を使用する場合。

ハンドブックや教科書などに種々の場合の応力集中係数がまとめられているが、公称応力の取り方に注意して利用する必要がある。

ひずみ集中

ひずみに関しても同様の係数、ひずみ集中係数(factor of strain concentration)が定義される[5]。

K ϵ = ϵ m a x ϵ n {\displaystyle K_{\epsilon }={\frac {\epsilon _{max}}{\epsilon _{n}}}}
ここで
Kε：ひずみ集中係数
εmax：最大ひずみ
εn：公称ひずみ

弾性範囲内ではKt=Kεだが、応力が降伏条件を満たして弾性範囲を脱すると、ひずみ集中係数は応力集中係数と異なってくる[6]。弾性範囲を超えると、塑性により応力集中は緩和されるが、ひずみ集中は緩和されない[5]。部材が静的負荷を受ける場合、切欠き底で弾性範囲を超えて塑性ひずみが生じるようになると、塑性領域での応力集中係数は弾性領域での応力集中係数よりも減少し、ひずみ集中係数は弾性領域よりも増大する[6]。

塑性範囲でのひずみ集中係数と応力集中係数の関係の推定式としては、ノイバー則(Neuber's rule)がよく用いられる[7]。ノイバー(Neuber)は、深い切欠きを有する部材が面外せん断を受ける場合の計算に基づいて次式の関係を導いた[7]。

K σ K ϵ = K t {\displaystyle {\sqrt {K_{\sigma }K_{\epsilon }}}=K_{t}}
ここで
Kt：弾性応力集中係数
Kσ：塑性応力集中係数
Kε：塑性ひずみ集中係数

ただし、有限要素法による検証によると、公称応力が材料の降伏応力を超えて切欠き底が全面降伏するような条件では、ノイバー則はひずみ集中係数にやや過大な値を与える傾向がある[6][8]。

2次元問題

実際の物体は3次元であるが、3次元物体の応力分布を求めるのは容易ではないので、厚みあるいは高さを0とした2次元の形状の応力解析が行われてきた。3次元物体が平面応力あるいは平面ひずみ状態にあるものを2次元問題として扱える。実際の物体では完全な平面応力あるいは平面ひずみにあるものは無いが、例えば薄板や高剛性材料に挟まれた物体などを、近似的に平面応力あるいは平面ひずみ状態と見なして2次元問題から得られた解や知見を当てはめることができる。弾性率が異なる別の物体が介在する場合を除き、2次元問題の応力分布は問題の物体の弾性率によらずに形状と境界条件(荷重条件、拘束条件)のみに依存する[9]。

以下に代表的な2次元形状の切欠きの応力集中の弾性解析解を示す。

円孔の応力集中

無限遠から一様引張応力を受ける無限板中の円孔による応力集中

遠方から一様な引張応力を受ける無限板に存在する円孔について、最大応力を含む線上での垂直応力分布は次式で与えられる[10]。

σ y = σ 0 ( 1 + a 2 2 x 2 + 3 a 4 2 x 4 ) {\displaystyle \sigma _{y}=\sigma _{0}\left(1+{\frac {a^{2}}{2x^{2}}}+{\frac {3a^{4}}{2x^{4}}}\right)}
ここで
σy：円孔中心を通り遠方応力に平行な線(x軸)上の垂直応力
σ0：遠方引張応力
a：円孔半径
x：円孔中心を通り遠方応力に平行な線(x軸)上の円孔中心からの距離

最大応力は上式でx = a(円孔縁)の位置で発生し、この点で円孔の応力集中係数は円孔半径の値によらず次のようになる。

K t = 3 {\displaystyle K_{t}=3}

楕円孔の応力集中

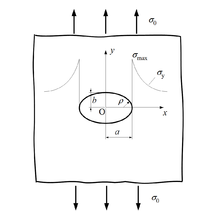
無限遠から一様引張応力を受ける無限板中の楕円孔による応力集中

遠方から長軸に垂直な一様引張応力を受ける無限板に存在する楕円孔について、最大応力を含む線上での応力分布は次式で与えられる[11]。

σ y = σ 0 [ 1 ξ 2 − 1 ( ξ 2 + a a − b ) − 1 ( ξ 2 − 1 ) 2 { ξ 2 2 ( a − b a + b − a + 3 b a − b ) − b ( a + b ) ( a − b ) 2 } − 4 ξ 2 ( ξ 2 − 1 ) 3 ( ξ 2 b a + b − b a − b ) a a − b ] {\displaystyle {\begin{aligned}\sigma _{y}=&\sigma _{0}{\bigg [}{\frac {1}{\xi ^{2}-1}}\left(\xi ^{2}+{\frac {a}{a-b}}\right)\\&-{\frac {1}{(\xi ^{2}-1)^{2}}}\left\{{\frac {\xi ^{2}}{2}}\left({\frac {a-b}{a+b}}-{\frac {a+3b}{a-b}}\right)-{\frac {b(a+b)}{(a-b)^{2}}}\right\}\\&-{\frac {4\xi ^{2}}{(\xi ^{2}-1)^{3}}}\left({\frac {\xi ^{2}b}{a+b}}-{\frac {b}{a-b}}\right){\frac {a}{a-b}}{\bigg ]}\\\end{aligned}}}
ξ = x + x 2 − c 2 c , c = a 2 − b 2 {\displaystyle \xi ={\frac {x+{\sqrt {x^{2}-c^{2}}}}{c}}\quad ,\quad c={\sqrt {a^{2}-b^{2}}}}
ここで
σy：楕円孔長軸(x軸)上の垂直応力
σ0：遠方引張応力
a：楕円孔長辺
b：楕円孔短辺
x：楕円孔長軸(x軸)上の楕円孔中心からの距離

最大応力は上式でx = a(楕円孔長辺縁)の位置で発生し、この点で応力集中係数は次のようになる。

K t = 1 + 2 a b {\displaystyle K_{t}=1+{\frac {2a}{b}}}

あるいはx = aの点における曲率半径を用いて次のようにも表される。

K t = 1 + 2 a ρ , ρ = b 2 / a {\displaystyle K_{t}=1+2{\sqrt {\frac {a}{\rho }}}\quad ,\quad \rho =b^{2}/a}

楕円孔は、b → 0とすればき裂（グリフィスき裂）の問題となり、また、等価楕円の概念を利用して任意形状の切欠きの応力集中系数を近似できる場合があるなど、他の問題への応用の広がりが大きい[12]。

等価楕円の概念

応力集中係数を概算するための等価楕円の概念、孔と切欠きの場合

理想的な円孔や楕円孔と異なる複雑な形状の孔や切欠きの応力集中係数を簡易に近似計算するために、等価楕円(equivalent ellipse)の考え方が平野により考案された[13]。等価楕円の考え方では、板中の孔に対しては孔の曲率半径ρと孔の全長2aと等しい楕円を、板縁切欠きに対しては切欠き底半径ρと切欠き深さaと等しい楕円を当てはめて応力集中係数を推定する。すなわち、これら2つのパラメータが応力集中に対しては影響が大きく、他の形状要素(例えば切欠きの開き角など)の影響は相対的に小さいと考える方法である[14]。

等価楕円による推定は万能ではなく、例えば、大きな孔縁にある非常に小さな切欠きの応力集中では、等価楕円による推定値は正確な応力集中係数値から大きく外れる[15]。ただし、上手く使用すれば実用上十分な近似値を推定できる。例えば遠方で引張を受ける無限板縁のV形切欠きの場合では、開き角がθ = 90°、切欠き深さと切欠き底半径の比がa/ρ = 4のときで、正確な数値計算結果ではKt = 5.274、等価楕円による計算ではKt = 5である[16]。

き裂の応力集中

無限遠から一様引張応力を受ける無限板中のき裂による応力集中

き裂の応力集中は楕円孔の短長をb → 0とした極限として考えることができる。遠方からき裂に垂直な一様引張応力を受ける無限板に存在する貫通直線き裂について、き裂延長線上での応力分布は次式で与えられる[17]。

σ y = σ 0 x x 2 − a 2 {\displaystyle \sigma _{y}={\frac {\sigma _{0}x}{\sqrt {x^{2}-a^{2}}}}}
ここで
σy：き裂延長線(x軸)上の垂直応力
σ0：遠方引張応力
a：き裂半長
x：き裂延長線(x軸)上のき裂中心からの距離

き裂先端の応力に注目すると、x → aではσy→∞となり、応力集中係数も∞となる。よってき裂の問題では、材料中の最大応力のみで材料強度を論じることができない。

さらに、上式をき裂先端を原点にx座標を取り直し、き裂先端近傍(x/a ≪ 1)に絞って考えると応力分布は次式となる。

σ y ≅ σ 0 a 2 x {\displaystyle \sigma _{y}\cong {\frac {\sigma _{0}{\sqrt {a}}}{\sqrt {2x}}}}
ここで
x：き裂延長線(x軸)上のき裂先端からの距離

上式から、き裂先端近傍部分の応力は x {\displaystyle {\sqrt {x}}} に反比例すること、応力分布はパラメータ σ 0 a {\displaystyle \sigma _{0}{\sqrt {a}}} により決定されることが分かる。 σ 0 a {\displaystyle \sigma _{0}{\sqrt {a}}} に π {\displaystyle {\sqrt {\pi }}} に乗じれば、破壊力学でき裂先端の応力状態を表すパラメータである応力拡大係数となる。

詳細は「破壊力学」、「応力拡大係数」、および「グリフィス理論」を参照

3次元問題

3次元問題の解析は2次元問題よりも非常に難しく、厳密解が得られる問題は非常に限られている。代わりにFEMによる数値解析が行われる。2次元問題の応力分布は、弾性係数が異なる別の物体が介在する場合を除き、問題の物体の弾性係数によらずに形状と境界条件のみにより決定されるが、3次元問題の場合は応力分布が物体の弾性係数(ポアソン比)にも依存する[18]。以下に3次元問題の代表的な切欠きの応力集中の弾性解析解を示す。

球状空洞による応力集中

無限遠から一様引張応力を受ける無限物体中の球状空洞による応力集中

遠方から一様引張応力を受ける無限物体に存在する球状空洞について、最大応力を含む面上での応力分布は次式で与えられる[2]。

σ z = σ 0 [ 1 + 4 − 5 ν 2 ( 7 − 5 ν ) a 3 r 3 + 9 2 ( 7 − 5 ν ) a 5 r 5 ] {\displaystyle \sigma _{z}=\sigma _{0}\left[1+{\frac {4-5\nu }{2(7-5\nu )}}{\frac {a^{3}}{r^{3}}}+{\frac {9}{2(7-5\nu )}}{\frac {a^{5}}{r^{5}}}\right]}
ここで
σz：球中心を通り遠方応力に平行な面(x-y面)上の垂直応力
σ0：遠方引張応力
a：球半径
r：球中心を通り遠方応力に平行な面(x-y面)上の球中心からの距離
ν：ポアソン比

最大応力は上式でr=a(球縁)の位置で発生し、この点で応力集中係数は次のようになる。

K t = 27 − 15 ν 2 ( 7 − 5 ν ) {\displaystyle K_{t}={\frac {27-15\nu }{2(7-5\nu )}}}

脚注

[脚注の使い方]

参考文献

  • 日本機械学会 編『機械工学辞典』（第2版）丸善、2007年1月20日。ISBN 978-4-88898-083-8。 
  • 日本材料学会 編『疲労設計便覧』（第3版）養賢堂、2008年10月1日。ISBN 978-4-8425-9501-6。 
  • 西田正孝『応力集中』（増補版）森北出版、1993年12月25日。ISBN 978-4-627-94029-1。 
  • 村上敬宜『弾性力学』（第14版）養賢堂、2004年3月30日。ISBN 978-4842501215。 
  • 村上敬宜『応力集中の考え方』（第1版）養賢堂、2005年7月1日。ISBN 978-4842503745。 
  • 左近淑郎, 伊達新吾「切欠きの非弾性応力・ひずみ集中の簡易推定法」『材料』第48巻、日本材料学会、1999年、30-37頁、doi:10.2472/jsms.48.30、ISSN 05145163、NAID 110002293614。 
  • 平野冨士夫「二次元彈性体の形状係数の研究(第2報)」『日本機械学會論文集』第55巻第16号、日本機械学、1950年11月5日、52-58頁、doi:10.1299/kikai1938.16.55_52、ISSN 00290270、NAID 110002349142。 

外部リンク

ウィキメディア・コモンズには、応力集中に関連するカテゴリがあります。