Filtr o nieskończonej odpowiedzi impulsowej

Filtr o nieskończonej odpowiedzi impulsowej (IIR filter ang. Infinite Impulse Response) – rodzaj filtru cyfrowego, który w odróżnieniu od filtrów FIR jest układem rekursywnym. IIR oznacza nieskończoną odpowiedź impulsową (w polskiej literaturze stosowana jest również nazwa filtr NOI). Znaczy to tyle, że reakcja na pobudzenie o skończonym czasie trwania jest teoretycznie nieskończenie długa. Jest to efektem występowania pętli sprzężenia zwrotnego widocznej na poniższym schemacie blokowym (zob. schemat filtru FIR).

Na powyższym schemacie moduły $z^{-1}$ oznaczają opóźnienie sygnału o jedną próbkę, natomiast $a_{i}$ oraz $b_{i}$ są współczynnikami filtru.

Transmitancję filtru IIR można opisać następująco:

H(z)={\frac {Y(z)}{X(z)}},

gdzie:

Y(z)

– transformata Z wyjścia,

X(z)

– transformata Z wejścia

lub po rozpisaniu wzorów na wielomiany opisujące bieguny i zera:

H(z)={\frac {a_{0}+a_{1}z^{-1}+\ldots +a_{p}z^{-p}}{1+(b_{1}z^{-1}+\ldots +b_{q}z^{-q})}}.

Zera transmitancji determinowane są przez miejsca zerowe wielomianu licznika, zaś miejsca zerowe wielomianu mianownika określają bieguny transmitancji.

Zalety i wady

Ze względu na dużą elastyczność w kształtowaniu przebiegu funkcji za pomocą ilorazu wielomianów, znacznie łatwiej uzyskać pożądaną charakterystykę używając filtru IIR niskiego rzędu niż filtru FIR. Wynikają z tego dwie podstawowe zalety filtrów IIR w porównaniu do FIR:

niska złożoność obliczeniowa,
niewielkie zapotrzebowanie na pamięć operacyjną.

Te zalety spowodowały duże zainteresowanie filtrami IIR i burzliwy rozwój teorii ich projektowania w latach 70. XX w., które przypadają na początki rozwoju technik cyfrowego przetwarzania sygnałów, gdy nie były dostępne procesory o odpowiedniej mocy obliczeniowej.

Do wad filtrów IIR należy zaliczyć:

Rekursywność filtru wprowadza potencjalne zagrożenie utraty stabilności (odpowiedź filtru w sposób niekontrolowany narasta do nieskończoności); niestabilność może mieć miejsce wtedy, gdy bieguny transmitancji (miejsca zerowe wielomianu w mianowniku) znajdą się poza okręgiem jednostkowym na płaszczyźnie zespolonej.
Projektowanie filtrów IIR jest znacznie trudniejsze niż w przypadku filtrów FIR – nie tylko ze względu na dodatkowy warunek zapewnienia stabilności.
Filtry IIR są znacznie bardziej wrażliwe na błędy zaokrągleń: zaokrąglenia wartości współczynników mogą znacząco zmienić charakterystykę, a zaokrąglenia wartości sygnału i wyników pośrednich wprowadzają szum, który może się akumulować.
Nie można ich zaimplementować jako filtrów o liniowej fazie, czyli takich, które wprowadzają takie samo opóźnienie grupowe dla wszystkich składowych częstotliwościowych przepuszczanego sygnału.

Z uwagi na rosnącą wydajność układów cyfrowych i procesorów sygnałowych, filtry IIR nie są obecnie tak chętnie wykorzystywane jak dawniej, a największą popularnością cieszą się filtry FIR, które nie mają wyżej wymienionych wad.

Przykład

Rozważane jest działanie filtru o nieskończonej odpowiedzi impulsowej. Założeniem jest estymacja średniego kosztu użytkowania energii elektrycznej na podstawie rachunku za prąd z bieżącego miesiąca $x(n)$ oraz oszacowanej wartości z poprzedniego miesiąca $y(n-1){:}$

y(n)={\frac {y(n-1)+x(n)}{2}}=0{,}5\cdot y(n-1)+0{,}5\cdot x(n),

gdzie:

n

– numer miesiąca,

x(n)

– wartość rachunku za bieżący miesiąc,

y(n)

– oszacowana wartość w bieżącym miesiącu,

y(n-1)

– oszacowanie wartości średniej w poprzednim miesiącu.

Dla $n=1$ pojawia się problem brzegowy, ponieważ nie dysponuje się oszacowaniem $y(0)$ – przyjęto, że $y(0)=0.$ Przykładowo:

y(1)=0{,}5\cdot x(1)+0{,}5\cdot y(0)=0{,}5\cdot 24+0{,}5\cdot 0=12

y(2)=0{,}5\cdot x(2)+0{,}5\cdot y(1)=0{,}5\cdot 12+0{,}5\cdot 27=19{,}5

Wartości kolejnych próbek wejściowych $x(n)$ (rachunków) oraz szacowanych wartości średnich $y(n)$ przedstawia tabela:

$n$	1	2	3	4	5	6	7	8	9	10	11	12
$x(n)$	24	27	31	59	33	37	0	0	0	0	0	0
$y(n)$	12	19,5	25,3	42,1	37,6	37,3	18,6	9,3	4,7	2,3	1,2	0,6

Wykres próbek wejściowych $x(n)$ oraz wyjściowych $y(n)$ przedstawiony jest na wykresie poniżej (sygnał określony jest tylko dla dyskretnych wartości $n,$ natomiast linie pomagają zaobserwować trend sygnału):

Na podstawie tego prostego przykładu można wysnuć następujące, użyteczne wnioski:

zaprojektowany filtr wygładza sygnał wejściowy – nagła zmiana sygnału wejściowego dla $n=4$ została stłumiona,
od chwili $n=7$ sygnał wejściowy $x(n)$ zanika – sygnał wyjściowy $y(n)$ dąży do zera, aczkolwiek tej wartości nigdy nie osiągnie – jest to cecha charakterystyczna filtrów o nieskończonej odpowiedzi impulsowej (NOI).

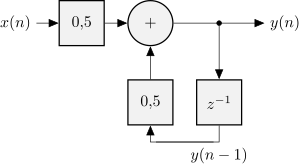
Realizację filtru z przykładu przestawiono na rysunku poniżej, gdzie blok opóźniający o jedną próbkę oznaczono przez $z^{-1}{:}$

Zobacz też

Bibliografia

Bartosz Ziółko, M. Ziółko: Przetwarzanie mowy. Wydawnictwa AGH, 2012.
Michał Tadeusiewicz: Signals and Systems. Wydawnictwo Politechniki Łódzkiej, 2004.
Przemysław Barański: Przekształcenie Z. Zastosowania w filtracji cyfrowej sygnałów – zbiór zadań. Wydawnictwo Politechniki Łódzkiej, 2014. ISBN 978-83-7283-638-0.