Equação de Butler-Volmer

Em eletroquímica, a equação de Butler-Volmer (em homenagem a John Alfred Valentine Butler^[1] e Max Volmer), também conhecida como equação de Erdey-Grúz-Volmer, é uma das relações mais fundamentais da cinética eletroquímica. Ela descreve como a corrente elétrica através de um eletrodo depende da diferença de potencial entre o eletrodo e a porção equipotencial do eletrólito para uma reação redox elementar, simples e rápida, considerando que ocorrem tanto uma reação catódica quanto uma anódica no mesmo eletrodo.^[2]

A equação de Butler-Volmer

A equação de Butler-Volmer corresponde à expressão abaixo:

${\displaystyle j=j_{0}\left[e^{{\frac {\alpha _{\rm {a}}zF}{RT}}(E-E_{\rm {eq}})}-e^{-{\frac {\alpha _{\rm {c}}zF}{RT}}(E-E_{\rm {eq}})}\right],}$

ou de uma forma mais compacta,

${\displaystyle j=j_{0}\left(e^{\frac {\alpha _{\rm {a}}zF\eta }{RT}}-e^{-{\frac {\alpha _{\rm {c}}zF\eta }{RT}}}\right),}$

em que atribuem-se as seguintes denotações:

• ${\displaystyle j}$: densidade de corrente do eletrodo [L^–2 I]
• ${\displaystyle j_{0}}$: densidade de corrente de troca [L^–2 I]
• ${\displaystyle E}$: potencial do eletrodo [T^–1 L² M I^–1]
• ${\displaystyle E_{\rm {eq}}}$: potencial de equilíbrio [T^–1 L² M I^–1]
• ${\displaystyle T}$: temperatura absoluta [Θ]
• ${\displaystyle z}$: número de elétrons envolvidos na reação do eletrodo [1]
• ${\displaystyle F}$: constante de Faraday [T I N]
• ${\displaystyle R}$: constante universal dos gases ideais [T^–2 L² M K^–1 N^–1]
• ${\displaystyle \alpha _{\rm {c}}}$: coeficiente de transferência de carga catódico [1]
• ${\displaystyle \alpha _{\rm {a}}}$: coeficiente de transferência de carga anódico [1]
• ${\displaystyle \eta }$ : sobrepotencial de ativação (definido como ${\displaystyle \eta =E-E_{\rm {eq}}}$) [T^–1 L² M I^–1].

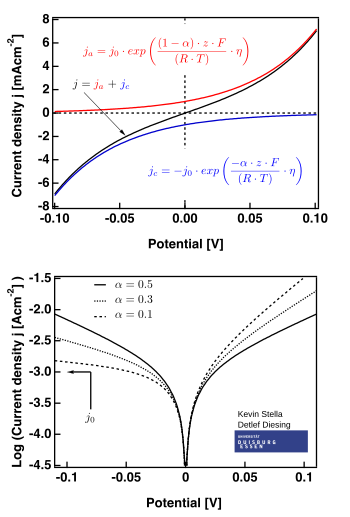
A figura à direita mostra situações nas quais ${\displaystyle \alpha _{\rm {a}}=1-\alpha _{\rm {c}}.}$

Os casos limite

Existem dois casos limite da equação de Butler-Volmer:

• a região de baixo sobrepotencial (chamada "resistência de polarização", em que ${\displaystyle E\approx E_{\mathrm {eq} }}$. Nela, a equação de Butler-Volmer pode ser simplificada pela aproximação mostrada abaixo:

  ${\displaystyle e^{x}\approx 1+x,\qquad |x|<<1,}$ da qual obtém-se a forma linear da equação:

  ${\displaystyle j=j_{0}{\frac {zF}{RT}}(E-E_{\rm {eq}});}$

• a região de alto sobrepotencial (em que ${\displaystyle \eta >>E_{\mathrm {eq} }}$), na qual a equação de Butler-Volmer converge para a equação de Tafel. Quando ${\displaystyle (E-E_{\rm {eq}})>>0}$, o primeiro termo dos parênteses domina e, quando ${\displaystyle (E-E_{\rm {eq}})<<0}$, o segundo termo domina.

Além disso, valem as relações:

${\displaystyle E-E_{\rm {eq}}=a_{\rm {c}}-b_{\rm {c}}\log j}$ para uma reação catódica, quando E<<E_eq, ou

${\displaystyle E-E_{\rm {eq}}=a_{\rm {a}}+b_{\rm {a}}\log j}$ para uma reação anódica, quando E>>E_eq,

em que ${\displaystyle a}$ e ${\displaystyle b}$ são constantes (para determinadas reação e temperatura) chamadas de constantes da equação de Tafel. Os valores teóricos das constantes da equação de Tafel são diferentes para os processos catódicos e anódicos. No entanto, a inclinação de Tafel ${\displaystyle b}$ pode ser definida como

${\displaystyle b=\left({\frac {\partial E}{\partial \ln |I_{\rm {F}}|}}\right)_{c_{i},T,p},}$

em que ${\displaystyle I_{\rm {F}}}$ é a corrente faradaica, expressa como ${\displaystyle I_{\rm {F}}=I_{\rm {c}}+I_{\rm {a}}}$, ou seja, a soma das correntes parciais catódica (${\displaystyle I_{\rm {c}}}$) e anódica (${\displaystyle I_{\rm {a}}}$).

A equação de Butler-Volmer estendida

A forma mais generalizada da equação de Butler-Volmer, aplicável às condições influenciadas pela transferência de massa, é apresentada abaixo:^[3]

${\displaystyle j=j_{0}\left[{\frac {c_{\rm {o}}(0,t)}{c_{\rm {o}}^{*}}}\cdot e^{\frac {\alpha _{\rm {a}}zF\eta }{RT}}-{\frac {c_{\rm {r}}(0,t)}{c_{\rm {r}}^{*}}}e^{-{\frac {\alpha _{\rm {c}}zF\eta }{RT}}}\right],}$

em que se adotam as seguintes denotações:

• ${\displaystyle j}$: densidade de corrente do eletrodo [L^–2 I]
• ${\displaystyle c_{\mathrm {o} }^{*}}$ e ${\displaystyle c_{\mathrm {r} }^{*}}$ são as concentrações, na porção majoritária da solução, das substâncias a serem oxidada e reduzida, respectivamente
• ${\displaystyle c_{\mathrm {o} }(0,t)}$ e ${\displaystyle c_{\mathrm {r} }(0,t)}$ são as concentrações dependentes do tempo, na porção da solução adjacente ao eletrodo, das substâncias a serem oxidada e reduzida, respectivamente.

A forma acima pode ser simplificada para a convencional (mostrada no início do artigo) quando a concentração da espécie eletroativa próximo à superfície do eletrodo é igual à sua concentração na porção majoritária da solução.

Existem duas taxas que determinam a relação corrente-tensão para um eletrodo. A primeira é a taxa da reação química no eletrodo, que consome reagentes e produz produtos. Isso é conhecido como taxa de transferência de carga. A segunda é a taxa na qual os reagentes são fornecidos e os produtos são removidos da região do eletrodo por vários processos, incluindo difusão, migração e convecção. Esta última é conhecida como taxa de transferência de massa. Essas duas taxas determinam as concentrações dos reagentes e produtos na região do eletrodo, parâmetros que, por sua vez, são determinados pelos próprios eletrodos. A mais lenta dessas taxas determina a taxa geral do processo. Por exemplo, se apenas a difusão contribuir para a taxa de transferência de massa, há uma taxa máxima na qual o reagente pode ser fornecido ao eletrodo e, portanto, a corrente possui um limite superior conhecido como corrente limitante. No caso de processos altamente controlados pela transferência de massa, o valor da densidade de corrente é dado por:

${\displaystyle j_{\text{máx}}={\frac {zFD_{\rm {ef}}}{\delta }}c^{*},}$

em que:

• ${\displaystyle D_{\mathrm {ef} }}$ é o coeficiente de difusão efetivo (considerando eventuais irregularidades do processo);
• ${\displaystyle \delta }$ é a espessura da camada de difusão;
• ${\displaystyle c^{*}}$ é a concentração da espécie eletroativa limitante na porção majoritária da solução.

A equação de Butler-Volmer simplificada assume que as concentrações no eletrodo são praticamente iguais às concentrações na porção majoritária do eletrólito, de modo que a corrente é expressa apenas em função do potencial. Em outras palavras, assume-se que a taxa de transferência de massa é muito maior que a taxa de transferência de carga e que a reação é dominada pela velocidade da reação química (mais lenta). Apesar dessa limitação, a utilidade da equação de Butler-Volmer na eletroquímica é ampla e muitas vezes é considerada "central na cinética fenomenológica do eletrodo".^[4]

A equação estendida de Butler-Volmer não faz essa suposição, mas considera as concentrações no eletrodo como dados conhecidos, produzindo uma relação na qual a corrente é expressa como uma função não apenas do potencial, mas também das concentrações fornecidas. A taxa de transferência de massa pode ser relativamente pequena, mas seu único efeito na reação química é através das diferenças entre as concentrações na porção majoritária da solução e na região próxima ao eletrodo (dados conhecidos). Com efeito, as concentrações também são uma função do potencial. Um tratamento completo, que expressa a corrente apenas em função do potencial, pode ser derivado da equação estendida de Butler-Volmer, mas exige o relacionamento explícito entre os efeitos de transferência de massa e o potencial da solução em cada ponto para que seja possível expressar as concentrações em função unicamente do potencial.

Dedução

Expressão geral

A seguinte derivação da equação estendida de Butler-Volmer é adaptada a partir das deduções de Bard e Faulkner^[3] e de Newman e Thomas-Alyea.^[5] Para uma reação elementar simples e rápida,

${\displaystyle {\ce {Ox + n\, e^{-}-> Red}}}$

As velocidades das reações direta e inversa (${\displaystyle v_{d}}$ e ${\displaystyle v_{i}}$) e as densidades de corrente elétrica associadas a elas (${\displaystyle j_{d}}$ e ${\displaystyle j_{i}}$) obtidas a partir das leis de Faraday podem ser escritas como:

${\displaystyle v_{d}=k_{d}\,c_{\mathrm {ox} }={\frac {j_{d}}{n\,F}},}$${\displaystyle v_{i}=k_{i}\,c_{red}={\frac {j_{i}}{n\,F}},}$

em que ${\displaystyle k_{d}}$ e ${\displaystyle k_{i}}$ são as constantes de velocidade das reações direta e inversa, respectivamente [T^–1] e ${\displaystyle c_{\mathrm {ox} }}$ e ${\displaystyle c_{\mathrm {red} }}$ são as concentrações superficiais das moléculas oxidada e reduzida no eletrodo, respectivamente [N L^–2] (denotapas por ${\displaystyle c_{\mathrm {o} }(0,t)}$ e ${\displaystyle c_{\mathrm {r} }(0,t)}$ na seção anterior). A velocidade líquida (${\displaystyle v}$) da reação de redução e a densidade de corrente líquida (${\displaystyle j}$) são, portanto,

${\displaystyle v=v_{d}-v_{i}={\frac {j_{d}-j_{i}}{n\,F}}={\frac {j}{n\,F}}.}$

Bard^[3] define uma corrente proporcional à velocidade líquida de oxidação, mas define o potencial ${\displaystyle E}$ como o potencial do eletrodo menos o potencial do eletrólito, o que tem o desconcertante (mas não inconsistente) efeito de designar uma corrente positiva para um potencial negativo. Na equação acima, é usada a convenção de Newman,^[5] na qual a corrente é escolhida proporcionalmente à velocidade líquida de redução, para manter correspondência com os resultados das seções anteriores.

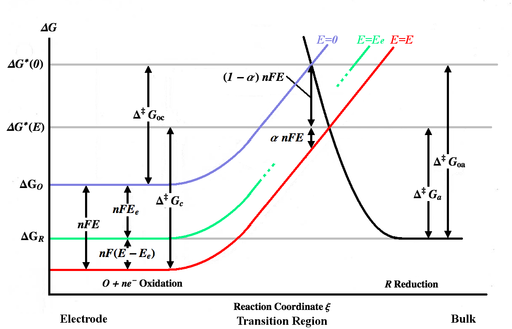
A figura acima representa várias curvas de energia livre de Gibbs em função da coordenada de reação ξ. A coordenada da reação pode ser aproximada para uma medida de distância, com o corpo do eletrodo à esquerda e a solução à direita. A curva azul mostra o aumento na energia livre de Gibbs para uma molécula oxidada conforme ela se aproxima da superfície do eletrodo quando nenhum potencial é aplicado. A curva de energia preta mostra o aumento da energia livre de Gibbs à medida que uma molécula reduzida se aproxima do eletrodo. As duas curvas de energia se cruzam em ${\displaystyle \Delta G^{*}(0)}$. A aplicação de um potencial ${\displaystyle E}$ ao eletrodo moverá a curva de energia livre de Gibbs da molécula oxidada para baixo (para a curva vermelha) por ${\displaystyle \Delta G=n\,F\,E}$ e o ponto de interseção se moverá para ${\displaystyle \Delta G^{*}(E)}$. Aumentar o potencial dos íons de zero para ${\displaystyle E}$ aumenta seu ${\displaystyle \Delta G}$ em ${\displaystyle E\,\Delta q}$, sendo ${\displaystyle \Delta q}$ a carga dos íons (ver potencial eletroquímico). Aumentar o potencial do eletrodo diminui o potencial dos íons próximos ao eletrodo em relação a ele, diminuindo, assim, seu ${\displaystyle \Delta G}$. ${\displaystyle \Delta ^{\ddagger }G_{\mathrm {c} }}$ e ${\displaystyle \Delta ^{\ddagger }G_{\mathrm {a} }}$ são as energias de ativação (barreiras energéticas) a serem superadas pelas espécies oxidada e reduzida, respectivamente, para um potencial ${\displaystyle E}$ qualquer, enquanto ${\displaystyle \Delta ^{\ddagger }G_{\mathrm {c,0} }}$ e ${\displaystyle \Delta ^{\ddagger }G_{\mathrm {a,0} }}$ são as energias de ativação para ${\displaystyle E=0}$. A curva de energia livre de Gibbs da molécula reduzida (curva preta) pode ser afetada pelo potencial, mas as conclusões não são invalidadas desde que a soma dos deslocamentos das curvas de oxidação e redução seja igual a ${\displaystyle n\,F\,E}$.^[5]

Assumindo-se que as constantes de velocidade obedecem à equação de Arrhenius, valem as seguintes relações:

${\displaystyle k_{d}=A_{d}\,e^{-{\frac {\Delta ^{\ddagger }G_{\mathrm {c} }}{RT}}},}$

${\displaystyle k_{i}=A_{i}\,e^{-{\frac {\Delta ^{\ddagger }G_{\mathrm {a} }}{RT}}},}$

nas quais ${\displaystyle A_{d}}$ e ${\displaystyle A_{i}}$ são constantes tais que ${\displaystyle A_{d}\,c_{\mathrm {ox} }=A_{i}\,c_{\mathrm {red} }}$ é a frequência de colisões com orientação favorável entre as moléculas oxidada e reduzida e os termos exponenciais (análogos aos fatores de Boltzmann) contabiliza a fração energeticamente favorável dessas colisões.

Supondo-se que as curvas sejam praticamente lineares na região de transição, elas podem ser representadas por:

${\displaystyle \Delta G=S_{\mathrm {c} }\,\xi +K_{\mathrm {c} }}$	(curva azul)
${\displaystyle \Delta G=S_{\mathrm {c} }\,\xi +K_{\mathrm {c} }-n\,F\,E}$	(curva vermelha)
${\displaystyle \Delta G=S_{\mathrm {a} }\,\xi +K_{\mathrm {a} }}$	(curva preta)

O coeficiente de transferência de carga para esse caso simples é equivalente ao fator de simetria e pode ser expresso em termos das inclinações das curvas:

${\displaystyle \alpha ={\frac {S_{\mathrm {c} }}{S_{\mathrm {a} }+S_{\mathrm {c} }}}.}$

Com isso, obtém-se as seguintes relações:

${\displaystyle \Delta ^{\ddagger }G_{\mathrm {c} }=\Delta ^{\ddagger }G_{\mathrm {c,0} }+\alpha \,n\,F\,E,}$

${\displaystyle \Delta ^{\ddagger }G_{\mathrm {a} }=\Delta ^{\ddagger }G_{\mathrm {a,0} }+(1-\alpha )\,n\,F\,E.}$

Por conveniência, define-se:

${\displaystyle f_{\alpha }={\frac {\alpha \,n\,F}{R\,T}},}$

${\displaystyle f_{\beta }={\frac {(1-\alpha )\,n\,F}{R\,T}},}$

${\displaystyle f=f_{\alpha }+f_{\beta }={\frac {n\,F}{R\,T}}.}$

As constantes de velocidade podem agora ser expressas como:

${\displaystyle k_{d}=k_{d,\mathrm {0} }\,e^{-f_{\alpha }\,E},}$

${\displaystyle k_{i}=k_{i,\mathrm {0} }\,e^{f_{\beta }\,E},}$

em que as constantes de velocidade no potencial ${\displaystyle E=0}$ são:

${\displaystyle k_{d,0}=A_{d}\,e^{-{\frac {\Delta ^{\ddagger }G_{\mathrm {c,0} }}{R\,T}}},}$

${\displaystyle k_{i,\mathrm {0} }=A_{i}\,e^{-{\frac {\Delta ^{\ddagger }G_{\mathrm {a,0} }}{R\,T}}}.}$

A densidade de corrente ${\displaystyle j}$ em função do potencial aplicado ${\displaystyle E}$ pode, então, ser escrita como:^[5]

${\displaystyle j=n\,F\,(c_{\mathrm {red} }\,k_{\mathrm {i,0} }\,e^{f_{\beta }\,E}-c_{\mathrm {ox} }\,k_{\mathrm {d,0} }\,e^{-f_{\alpha }\,E}).}$

Expressão em termos do potencial de equilíbrio

A uma certa tensão ${\displaystyle E_{\mathrm {eq} }}$, o equilíbrio será atingido e as velocidades das reações direta e inversa (${\displaystyle v_{d}}$ e ${\displaystyle v_{i}}$) serão iguais. Isso é representado pela curva verde na figura acima. As constantes de velocidade de equilíbrio serão escritas como ${\displaystyle k_{d,\mathrm {eq} }}$ e ${\displaystyle k_{i,\mathrm {eq} }}$, e as concentrações de equilíbrio serão denotadas por ${\displaystyle c_{\mathrm {ox,eq} }}$ e ${\displaystyle c_{\mathrm {red,eq} }}$. As densidades de corrente no equilíbrio (${\displaystyle j_{\mathrm {ox,eq} }}$ e ${\displaystyle j_{\mathrm {red,eq} }}$) serão ambas iguais a ${\displaystyle j_{\mathrm {o} }}$, a chamada densidade de corrente de troca.

${\displaystyle v_{d,\mathrm {eq} }\,=k_{d,\mathrm {eq} }\,c_{\mathrm {ox,eq} }={\frac {j_{\mathrm {o} }}{n\,F}},}$

${\displaystyle v_{i,\mathrm {eq} }\,=k_{i,\mathrm {eq} }\,c_{\mathrm {red,eq} }={\frac {j_{\mathrm {o} }}{n\,F}}.}$

Observe-se que a densidade de corrente líquida no equilíbrio torna-se nula. As constantes de velocidade de equilíbrio são, portanto, dadas por:

${\displaystyle k_{d,\mathrm {eq} }=k_{d,0}\,e^{-f_{\alpha }\,E_{\mathrm {eq} }},}$

${\displaystyle k_{i,\mathrm {eq} }=k_{i,0}\,e^{f_{\beta }\,E_{\mathrm {eq} }}.}$

Tratando o sistema acima para ${\displaystyle k_{d,0}}$ e ${\displaystyle k_{i,0}}$ em termos das concentrações de equilíbrio ${\displaystyle c_{\mathrm {ox,eq} }}$ e ${\displaystyle c_{\mathrm {red,eq} }}$ e da densidade de corrente de troca ${\displaystyle j_{\mathrm {o} }}$, a densidade de corrente ${\displaystyle j}$ como uma função do potencial aplicado ${\displaystyle E}$ pode ser escrita:^[5]

${\displaystyle j=j_{\mathrm {o} }\left[{\frac {c_{\mathrm {red} }}{c_{\mathrm {red,eq} }}}\,e^{f_{\beta }\,(E-E_{\mathrm {eq} })}-{\frac {c_{\mathrm {ox} }}{c_{\mathrm {ox,eq} }}}\,e^{-f_{\alpha }\,(E-E_{\mathrm {eq} })}\right].}$

Assumindo que a porção majoritária da solução se mantém em equilíbrio, com concentrações ${\displaystyle c_{\mathrm {ox} }^{*}}$ e ${\displaystyle c_{\mathrm {red} }^{*}}$, tem-se que ${\displaystyle c_{\mathrm {ox,eq} }=c_{\mathrm {ox,eq} }^{*}}$ e ${\displaystyle c_{\mathrm {red,eq} }=c_{\mathrm {red,eq} }^{*}}$, e a expressão acima para a densidade de corrente ${\displaystyle j}$ se reduz à equação de Butler-Volmer. A diferença ${\displaystyle E-E_{\mathrm {eq} }}$ é conhecida como sobrepotencial de ativação (denotado por ${\displaystyle \eta }$).

Expressão em termos do potencial formal

Para a reação simplificada mostrada anteriormente, a variação da energia de Gibbs é dada por:

${\displaystyle \Delta G=\Delta G_{\mathrm {ox} }-\Delta G_{\mathrm {red} }=(\Delta G_{\mathrm {ox} }^{o}-\Delta G_{\mathrm {red} }^{o})+R\,T\,\ln {\left({\frac {a_{\mathrm {ox,eq} }}{red,eq}}\right)},}$

em que ${\displaystyle a_{\mathrm {ox,eq} }}$ e ${\displaystyle a_{\mathrm {red,eq} }}$ são as atividades no equilíbrio. Note-se que a variação na energia livre de Gibbs também é igual a ${\displaystyle \Delta ^{\ddagger }G_{oa}-\Delta ^{\ddagger }G_{oc}}$. As atividades ${\displaystyle a}$ estão relacionadas às concentrações ${\displaystyle c}$ por ${\displaystyle a=\gamma \,c}$, sendo ${\displaystyle \gamma }$ o coeficiente de atividade. O potencial de equilíbrio é dado pela equação de Nernst:

${\displaystyle E_{\mathrm {eq} }=-{\frac {\Delta G}{n\,F}}=E^{o}+{\frac {R\,T}{n\,F}}\ln {\left({\frac {a_{\mathrm {ox,eq} }}{a_{\mathrm {red,eq} }}}\right)},}$

em que ${\displaystyle E^{o}}$ é o potencial padrão.

${\displaystyle E^{o}=-{\frac {\Delta G_{\mathrm {ox} }^{o}-\Delta G_{\mathrm {red} }^{o}}{n\,F}}.}$

Definindo o potencial formal como^[3]

${\displaystyle E^{o}=-{\frac {\Delta G_{\mathrm {ox} }^{o}-\Delta G_{\mathrm {red} }^{o}}{n\,F}}.}$

o potencial de equilíbrio é, então, dado por:

${\displaystyle E_{\mathrm {eq} }=E^{o\,\prime }+{\frac {R\,T}{n\,F}}\ln {\left({\frac {c_{\mathrm {red,eq} }}{c_{\mathrm {red,eq} }}}\right)}.}$

Substituindo esse potencial de equilíbrio na equação de Butler-Volmer, obtém-se:

${\displaystyle j={\frac {j_{0}}{c_{\mathrm {ox,eq} }^{1-\alpha }\,c_{\mathrm {red,eq} }^{\alpha }}}\left[c_{\mathrm {red} }\,e^{f_{\beta }(E-E^{o\,\prime })}-c_{\mathrm {ox} }\,e^{-f_{\alpha }(E-E^{o\,\prime })}\right],}$

que também pode ser escrita em termos da constante de velocidade padrão ${\displaystyle k^{o}}$ como:^[3]

${\displaystyle j=n\,F\,k^{o}\left[c_{\mathrm {red} }\,e^{f_{\beta }(E-E^{o\,\prime })}-c_{\mathrm {ox} }\,e^{-f_{\alpha }(E-E^{o\,\prime })}\right].}$

A constante de velocidade padrão é um importante descritor do comportamento do eletrodo independente das concentrações. É uma medida da velocidade na qual o sistema se aproxima do equilíbrio. No limite, à medida que ${\displaystyle k^{o}\rightarrow 0}$, o eletrodo se torna um eletrodo polarizável ideal e se comporta eletricamente como um circuito aberto (desconsiderando a capacitância). Para eletrodos quase ideais com ${\displaystyle k^{o}}$ pequeno, grandes mudanças no sobrepotencial são necessárias para gerar uma corrente significativa. À medida que ${\displaystyle k^{o}\rightarrow \infty }$, o eletrodo torna-se um eletrodo não-polarizável ideal e se comporta como um sistema em curto-circuito. Para eletrodos quase ideais com altos valores de ${\displaystyle k^{o}}$, pequenas mudanças no sobrepotencial geram grandes mudanças na corrente.

Ligações externas

• Media relacionados com Equação de Butler-Volmer no Wikimedia Commons

Ver também

• Equação de Nernst
• Equação de Goldman-Hodgkin-Katz

Referências