Insieme complemento

Nella teoria degli insiemi e in altri campi della matematica, il complemento di un insieme è l'insieme degli elementi che non appartengono a quell'insieme. Gli insiemi complemento si dividono nei complementi relativi (detti anche insieme differenza) e nei complementi assoluti.

Complemento relativo

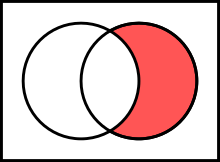
Avendo due insiemi ${\displaystyle A}$ e ${\displaystyle B}$, il complemento di ${\displaystyle A}$ rispetto a ${\displaystyle B}$ o l'insieme differenza ${\displaystyle B}$ meno ${\displaystyle A}$, è formato dai soli elementi di ${\displaystyle B}$ che non appartengono ad ${\displaystyle A}$. Esso si indica solitamente come ${\displaystyle B\setminus A}$ oppure come ${\displaystyle B-A}$. Formalmente abbiamo:

${\displaystyle B\setminus A=B-A=\{x\in B\wedge x\notin A\}}$

Si noti che l'insieme differenza ${\displaystyle B-A}$ è un sottoinsieme dell'insieme ${\displaystyle B}$.

Esempi

• ${\displaystyle \lbrace 1,2,3,4,5\rbrace -\lbrace 3\rbrace =\lbrace 1,2,4,5\rbrace }$
• ${\displaystyle \lbrace a,b,c,d\rbrace -\lbrace c,d,e,f\rbrace =\lbrace a,b\rbrace }$
• ${\displaystyle \lbrace 1,2,3\rbrace -\lbrace 2,3,4\rbrace =\lbrace 1\rbrace }$
• ${\displaystyle \lbrace 2,3,4\rbrace -\lbrace 1,2,3\rbrace =\lbrace 4\rbrace }$

Proposizioni

Se ${\displaystyle A}$, ${\displaystyle B}$ e ${\displaystyle C}$ sono insiemi, allora valgono le seguenti identità:

• ${\displaystyle C-\left(A\cap B\right)=\left(C-A\right)\cup \left(C-B\right)}$
• ${\displaystyle C-\left(A\cup B\right)=\left(C-A\right)\cap \left(C-B\right)}$
• ${\displaystyle C-(B-A)=(A\cap C)\cup (C-B)}$
• ${\displaystyle (B-A)\cap C=(B\cap C)-A=B\cap (C-A)}$
• ${\displaystyle (B-A)\cup C=(B\cup C)-(A-C)}$
• ${\displaystyle A-A=\varnothing }$
• ${\displaystyle \varnothing -A=\varnothing }$
• ${\displaystyle A-\varnothing =A}$

Complemento assoluto

Il complemento assoluto è un caso particolare del complemento relativo.

Se è definito un insieme universo ${\displaystyle U}$, si definisce complemento assoluto di ${\displaystyle A}$ come il complemento relativo di ${\displaystyle A}$ rispetto ad ${\displaystyle U}$. Formalmente abbiamo:

${\displaystyle A^{c}=\neg A=U-A=\{x\in U{\text{ e }}x\notin A\}}$

Il complemento assoluto, indicato anche come ${\displaystyle \sim A}$, rappresenta anche il NOT nell'algebra Booleana.

A titolo di esempio, se l'insieme universale è l'insieme dei numeri naturali, allora il complemento dell'insieme dei numeri dispari è l'insieme dei numeri pari.

La prossima proposizione riporta alcune proprietà fondamentali del complemento assoluto in rapporto alle operazioni insiemistiche di unione e intersezione.

Se ${\displaystyle A}$ e ${\displaystyle B}$ sono sottoinsiemi di un insieme universo ${\displaystyle U}$, allora valgono le seguenti identità.

Leggi di De Morgan:

• ${\displaystyle (A\cup B)^{c}=A^{c}\cap B^{c};}$
• ${\displaystyle (A\cap B)^{c}=A^{c}\cup B^{c}.}$

Leggi di complementarità:

• ${\displaystyle A\cup A^{c}=U;}$
• ${\displaystyle A\cap A^{c}=\varnothing ;}$
• ${\displaystyle \varnothing ^{c}=U;}$
• ${\displaystyle U^{c}=\varnothing ;}$
• Se ${\displaystyle A\subseteq B}$, allora ${\displaystyle B^{c}\subseteq A^{c}}$ (ciò segue dall'equivalenza di una proposizione condizionale con la proposizione contronominale).

Involuzione o legge del doppio complemento:

• ${\displaystyle (A^{c})^{c}=A.}$

Relazioni tra complemento relativo e complemento assoluto:

• ${\displaystyle A-B=A\cap B^{c};}$
• ${\displaystyle (A-B)^{c}=A^{c}\cup B.}$

Le prime due leggi di complementarità mostrano che se ${\displaystyle A}$ è un sottoinsieme non vuoto di ${\displaystyle U}$, allora ${\displaystyle \{A,A^{c}\}}$ è una partizione di ${\displaystyle U}$.

Bibliografia

• Seymour Lipschutz, Topologia, Sonzogno, Etas Libri, 1979.
• (EN) Paul Halmos (1960): Naive set theory, D. Van Nostrand Company. Ristampato da Springer nel 1974, ISBN 0-387-90092-6.
• (FR) Nicolas Bourbaki (1968): Théorie des ensembles, Hermann.

Voci correlate

• Unione
• Intersezione
• Differenza simmetrica
• Sottoclasse
• Teoria degli insiemi

Collegamenti esterni

• (EN) complement, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Insieme complemento / Insieme complemento (altra versione), su MathWorld, Wolfram Research.

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica