Paradoxe du train

Cet article ne s'appuie pas, ou pas assez, sur des sources secondaires ou tertiaires (juin 2023).

Pour améliorer la vérifiabilité de l'article ainsi que son intérêt encyclopédique, il est nécessaire, quand des sources primaires sont citées, de les associer à des analyses faites par des sources secondaires.

Le paradoxe du train est une expérience de pensée destinée à illustrer des effets paradoxaux de la relativité restreinte : non-pertinence des notions de simultanéité et d'antériorité absolues et contraction des longueurs.

Description du paradoxe

La situation apparemment incohérente présentée par le paradoxe du train est la suivante. Considérons un train animé d'une vitesse v proche de celle de la lumière (ce qui est évidemment impossible à réaliser concrètement) et un tunnel ayant la même longueur propre (c'est-à-dire mesurée dans un repère au repos par rapport à l'objet mesuré). La relativité restreinte indique que si nous mesurons la longueur du train depuis la voie ou le tunnel, le train avec sa vitesse relative v apparaîtra plus court que le tunnel du facteur de Lorentz :

${\displaystyle \gamma =1/{\sqrt {1-v^{2}/c^{2}}}}$

La situation vue du train est différente : dans le référentiel du train, le tunnel étant animé d'une vitesse -v paraît plus court (du même rapport ${\displaystyle \gamma }$) que le train. Le tunnel ne semble donc pas susceptible de contenir le train dans toute sa longueur.

Il en résulte que pour les observateurs situés sur la voie, l'arrière du train sera déjà dans le tunnel quand l'avant en sortira. Pour les passagers du train, c'est l'inverse : l'avant sortira du tunnel alors que l'arrière n'y sera pas encore entré.

Imaginons alors l'expérience suivante : une bombe est située à l'avant du train, prête à exploser au moment précis où le train sort du tunnel. En même temps cette bombe peut être désamorcée grâce à un signal émis à l'arrière du train au moment précis où la queue du convoi entre dans le tunnel. La bombe éclatera-t-elle ou non ?

Dans le repère de la voie, l'arrière du train entre dans le tunnel avant que l'avant soit sorti. Le signal de désamorçage est émis et neutralise l'explosion : la bombe n'explose pas.

Dans le repère du train l'avant du train sort avant que l'arrière soit entré. Donc le signal de désamorçage ne peut pas atteindre l'avant : la bombe explose.

La bombe ne peut pas à la fois exploser et ne pas exploser selon le repère choisi. La relativité restreinte serait-elle en défaut ?

Contraction des longueurs

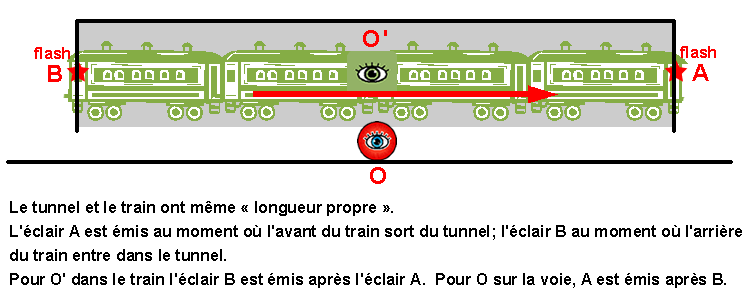
Supposons que le tunnel soit équipé de deux détecteurs, un à l'entrée E et l'autre à la sortie S. Le train, supposé se déplacer à une vitesse proche de celle de la lumière, traverse ce tunnel. Le détecteur de sortie émet un signal lumineux A lorsque l'avant P du train sort du tunnel. Le détecteur d'entrée émet un signal lumineux B lorsque l'arrière Q du train entre dans le tunnel. Autrement dit, l'événement A consiste dans le passage du point P du train devant le point S de la voie et l'événement B dans le passage du point Q du train devant le point E de la voie.

La relativité restreinte indique que, vu de la voie, le train paraît raccourcir. Cela veut dire que, pour les observateurs fixes, lorsque l'arrière Q du train entre dans le tunnel, l'avant P n'en est pas encore sorti. Autrement dit, l'éclair A est émis après l'éclair B de désamorçage. Si l'observateur O sur la voie est à mi-distance des extrémités du tunnel, il recevra donc d'abord l'éclair B (et à cet instant tout le train sera à l'intérieur du tunnel) puis un bref instant après l'éclair A.

La vision des passagers du train est différente. Pour eux, c'est le tunnel qui paraît plus court que leur train. Cela revient à dire que lorsque l'avant P du train est sorti du tunnel (éclair A), l'arrière Q du train n'y est pas encore entré (éclair B). Par conséquent, l'ordre des événements A et B est inversé par rapport aux observateurs de la voie. L'événement A précède maintenant l'événement B. Un passager situé au milieu du train recevra l'éclair A avant l'éclair B de désamorçage.

Il n'y a rien d'incohérent à ces différences de point de vue entre l'observateur au repos et l'observateur en mouvement. La relativité restreinte affirme en effet que les notions d'antériorité et de simultanéité sont relatives, c'est-à-dire dépendent du référentiel dans lequel on fait les mesures. Elles n'ont pas de caractère absolu. Depuis la voie, A est postérieur à B tandis que depuis le train B est postérieur à A.

Résolution du paradoxe

Revenons alors à la question posée^{[style à revoir]}. L'événement A correspond à l'explosion de la bombe placée à l'avant du train, l'événement B à celui de l'émission du signal de désamorçage de la bombe. Dans le repère du train, il n'y a aucune ambiguïté : l'événement B étant postérieur à A, le signal de désamorçage B est émis alors que la bombe a déjà explosé. Dans le repère de la voie, le signal B est émis avant que la bombe n'explose. Mais ce signal aura-t-il le temps de parvenir jusqu'à l'avant du train ? La réponse est négative, de sorte que la bombe explosera. On peut le montrer de plusieurs façons.

La relativité restreinte définit le carré de l'intervalle spatio-temporel entre deux événements A et B séparés par une distance temporelle Δt et une distance spatiale Δl par la formule

${\displaystyle \,c^{2}\Delta \tau ^{2}=c^{2}\Delta t^{2}-\Delta l^{2}}$

et énonce que cette quantité est indépendante du repère dans lequel elle est évaluée. En particulier, elle peut être positive ou négative mais ce caractère ne dépend pas du système de coordonnées choisi (contrairement aux notions de simultanéité ou d'équidistance qui sont quant à elles relatives).

Si la quantité est négative, cela signifie que l'intervalle est du type « espace » (la distance spatiale est plus grande que la distance temporelle) et implique alors que les événements A et B sont indépendants l'un de l'autre. Or puisque nous venons de voir que B n'a pas pu agir sur A quand on se place dans le repère du train, il en est nécessairement de même dans le repère de la voie ferrée^{[note 1]}. Cela veut dire à son tour que le signal émis par l'arrière du train n'aura pas le temps d'arriver à l'avant pour empêcher l'explosion de la bombe. Dans le repère de la voie, les observateurs fixes concluront donc également que la bombe explosera.

Il n'y a ainsi pas de contradiction dans l'analyse de la relativité restreinte.

Explication qualitative

Le signal B doit dans tous les cas traverser la totalité de la longueur propre L du train.

Or depuis la voie la longueur L se contracte en ${\displaystyle L/\gamma }$: certes plus ${\displaystyle v}$ sera élevée plus l'avant P sera perçu éloigné de la sortie S à l'émission du signal B; mais par ailleurs P se rapprochera alors d'autant plus rapidement de S : la longueur L ne se contracte ainsi "pas suffisamment" (en ${\displaystyle v/\gamma }$) pour empêcher l'avant P de rejoindre (en ${\displaystyle v}$) la sortie S.

Les calculs suivants développent quantitativement ce raisonnement et fournissent tous les détails du problème.

Explication quantitative

Formulation complète du problème

Considérons un train PQ de longueur propre L, P étant l'avant et Q l'arrière. Si on choisit l'arrière du train comme origine des coordonnées spatiales dans ce repère, les abscisses des extrémités sont :

${\displaystyle {\begin{cases}\,x'_{P}=L\\x'_{Q}=0\,.\end{cases}}}$

Considérons maintenant un tunnel ES de même longueur L que le train mesurée dans le repère fixe. E est l'entrée du tunnel, S la sortie. Dans ce repère « fixe », l'entrée du tunnel est prise comme origine des coordonnées spatiales de sorte que les abscisses de E et S sont

${\displaystyle {\begin{cases}\,x_{E}=0\\x_{S}=L\,.\end{cases}}}$

Le temps dans le repère du train sera mesuré par la quantité t ’, et dans le repère de la voie par la quantité t.

L'événement « émission du signal B », celui qui marque la coïncidence du point Q avec E, c'est-à-dire l'entrée de l'arrière du train dans le tunnel) sera pris comme origine des coordonnées. Par convention on a donc :

${\displaystyle \,x_{B}=t_{B}=x'_{B}=t'_{B}=0\,.}$

L'événement « émission du signal A », qui marque la coïncidence de P avec S, c'est-à-dire la sortie de l'avant du train, est déterminé par

${\displaystyle x_{A}=x'_{A}=L\,.}$.

Si la vitesse du train est v par rapport aux observateurs fixes situés sur la voie ferrée, les formules de Lorentz, qui permettent de passer des coordonnées (x ’, t ’) mesurées dans le train aux coordonnées (x, t ) mesurées sur la voie, s'écrivent :

${\displaystyle {\begin{cases}ct=\gamma (ct'+\beta x')\\x=\gamma (x'+\beta ct')\end{cases}}}$

où β et γ sont les quantités usuelles

${\displaystyle \beta \,=\,v/c}$   et   ${\displaystyle \gamma \,=[1-(v^{2}/c^{2})]^{-1/2}\equiv 1/{\sqrt {1-\beta ^{2}}}\,.}$

D'après les formules précédentes, les coordonnées des extrémités P et Q du train dans le repère de la voie ferrée s'expriment sous la forme :

${\displaystyle {\begin{cases}ct=\gamma (ct'+\beta L)\\x_{P}=\gamma (L+\beta ct')\end{cases}}}$

et

${\displaystyle {\begin{cases}ct=\gamma (ct')\\x_{Q}=\gamma (\beta ct')\,.\end{cases}}}$

En éliminant t ' dans ces équations on aboutit à l'équation du mouvement de P et Q dans le repère fixe de la voie :

${\displaystyle {\begin{cases}x_{P}=vt+L{\sqrt {1-\beta ^{2}}}\equiv vt+L/\gamma \\x_{Q}=vt\,.\end{cases}}}$

Incidemment on retrouve le facteur de contraction des longueurs de Lorentz 1/γ en vérifiant qu'au même instant t (par exemple en t = 0) la différence (x_P - x_Q), qui représente la longueur du train dans le repère fixe, est égale à L /γ.

Les équations précédentes fournissent alors les coordonnées temporelle et spatiale de l'événement A comme

${\displaystyle t_{A}=(L/v)(1-\gamma ^{-1})\equiv (L/v)\left(1-{\sqrt {1-\beta ^{2}}}\right)\ ,\ x_{A}=L}$

Comme annoncé on constate que depuis la voie l'instant t _A du signal A de sortie du tunnel est postérieur à l'instant du signal indiquant l'entrée dans le tunnel de la queue du train (le train est plus court que le tunnel). La différence de temps entre les deux événements A et B est

${\displaystyle \Delta t=(L/v)\left(1-{\sqrt {1-\beta ^{2}}}\right)}$

Lorsque β est assez petit on peut développer l'expression au premier ordre pour obtenir

${\displaystyle \Delta t\simeq Lv/(2c^{2})\,.}$

Comment les choses se mesurent-elles dans le repère du train ? Les formules inverses permettant de passer des coordonnées fixes aux coordonnées mobiles (pour dire les choses rapidement) sont :

${\displaystyle {\begin{cases}ct'=\gamma (ct-\beta x)\\x'=\gamma (x-\beta ct)\end{cases}}}$

Après un calcul identique au précédent on obtient les coordonnées de l'événement A dans le repère du train comme

${\displaystyle t'_{A}=-(L/v)(1-\gamma ^{-1})\equiv -(L/v)\left(1-{\sqrt {1-\beta ^{2}}}\right)\ ,}$

On constate que l'ordre temporel des événements est inversé dans le repère du train par rapport au repère de la voie. Maintenant t ’_A est négatif, ce qui signifie que l'avant du train sort du tunnel avant que l'arrière y soit entré (pour les voyageurs le tunnel est plus court que le train). La situation est parfaitement symétrique puisque

${\displaystyle t'_{A}=-t_{A}\ .}$

Tout est cohérent. Le paradoxe du train dans le tunnel n'est pas signe que la relativité restreinte serait fausse.

Revenons enfin à la question de savoir si la bombe prête à exploser quand le train sort du tunnel le fera ou non. Calculons à cet effet le carré de l'intervalle spatio-temporel

${\displaystyle \,c^{2}\Delta \tau ^{2}=c^{2}t_{A}^{2}-L^{2}=c^{2}{t'_{A}}^{2}-L^{2}\,.}$

On trouve

${\displaystyle \,c^{2}\Delta \tau ^{2}=-2(L^{2}/\beta ^{2}){\sqrt {1-\beta ^{2}}}\left(1-{\sqrt {1-\beta ^{2}}}\right)<0\,.}$

Cette quantité est le fameux invariant de la relativité restreinte, c'est-à-dire qu'elle ne dépend pas du repère dans lequel on la calcule. Elle reste notamment négative quel que soit le repère considéré, ce qui montre que les deux événements A et B ne peuvent pas être liés par un lien de cause à effet, dans aucun repère. L'intervalle d'espace-temps entre les deux événements A et B est dit du « genre espace ».

Vérifions directement en faisant le calcul dans le repère de la voie que le signal de désamorçage B n'a pas le temps d'atteindre l'avant du train avant l'explosion de la bombe. Le temps nécessaire pour que le signal (voyageant à la vitesse c) aille de l'arrière à l'avant est

${\displaystyle \,t_{\text{voulu}}=L/c\,,}$

tandis que le temps disponible est

${\displaystyle \,t_{\text{dispo}}=t_{A}=L/(\beta c)\left(1-{\sqrt {1-\beta ^{2}}}\right)\,.}$

On constate que

${\displaystyle \,t_{\text{dispo}}-\,t_{\text{voulu}}=L/(\beta c)\left(1-{\sqrt {1-\beta ^{2}}}-\beta \right)={\frac {L}{\beta c}}{\sqrt {1-\beta }}\left({\sqrt {1-\beta }}-{\sqrt {1+\beta }}\right)<0}$

Le fait que le temps disponible soit inférieur au temps nécessaire signifie bien que le signal B n'a pas le temps d'atteindre la bombe pour la désamorcer avant qu'elle explose.

Dans les deux repères la conclusion est la même : les deux événements « explosion de la bombe » et « envoi du signal de désamorçage » sont causalement indépendants. Par conséquent les passagers du train comme les observateurs fixes de la voie concluent que la bombe explosera.

 

Illustration graphique du paradoxe

Diagramme d'espace-temps

Le schéma ci-contre représente le passage du train dans le tunnel dans un diagramme espace-temps^[1]. Y sont représentées les lignes d'univers d'une part de l'avant P du train et de l'arrière Q du train, et d'autre part de la sortie S du tunnel et de son entrée E.

Lorsque l'avant P du train coïncide avec la sortie S, c'est l'événement A. Lorsque l'arrière Q du train coïncide avec l'entrée E du tunnel, c'est l'événement B. Les coordonnées (x, t) correspondent au repère fixe de la voie. Les coordonnées (x′, t′) sont relatives au train. L'origine des coordonnées peut être choisie de façon arbitraire. (Pour fixer les idées on peut prendre l'événement B comme origine avec t_B = t′_B = 0.)

Le temps t_A ou t′_A correspondant à l'événement A est obtenu en menant de A la parallèle à l'axe x ou x′ et en notant où cette parallèle coupe l'axe temporel. On remarque immédiatement que t_A est supérieur à t_B tandis que t′_A est inférieur à t′_B. Autrement dit l'événement A est postérieur à l'événement B pour les observateurs situés sur la voie tandis que l'inverse est vrai pour les passagers du train, ces derniers jugeant que l'événement A est antérieur à B. On a démontré précédemment, algébriquement, que l'écart temporel entre A et B est le même en valeur absolue dans les deux repères, bien que le signe diffère.

Le diagramme montre encore que l'événement A est situé à l'extérieur du cône de lumière issu de l'événement B. Autrement dit les événements A et B ne peuvent pas être liés par un quelconque lien de cause à effet. La distance spatiale les séparant est trop grande devant leur distance temporelle, de sorte qu'un signal issu de A ne peut pas atteindre l'événement B avant que ce dernier se produise (et réciproquement).

La droite joignant les événements A et B représente l'axe des abscisses dans un repère particulier, celui où ces deux événements ont lieu au même instant^{[note 2]}. La vitesse w de ce repère par rapport à la voie ferrée est inférieure à la vitesse du train. Dans un autre repère, quelconque, l'événement A sera antérieur à B si sa vitesse est supérieure à w (c'est le cas du train) et sera postérieur à B si sa vitesse est inférieure à w (c'est le cas du repère de la voie ferrée).

Pour éviter les fausses interprétations des effets de relativité restreinte, redisons que la contraction de longueur évoquée ici n'est pas réaliste pour un vrai train ! Les effets de relativité restreinte dépendent du fameux facteur de Lorentz γ et ne deviennent notables que lorsque les vitesses approchent celle de la lumière, ce qui n'est pas le cas de la vitesse d'un train, qui reste inférieure à 3 × 10^-7 c (90 m/s, soit 1 080 km/h).

Animation

Le dessin animé ci-contre montre le passage du train dans le tunnel dans chacun des deux repères.

La partie d'en-bas décrit le passage du train dans le repère du tunnel : le premier signal indique l'entrée de l'arrière du train dans le tunnel alors que le second marque la sortie de l'avant du train. Le signal émis par l'arrière du train n'a pas le temps d'atteindre l'avant.

La partie d'en-haut décrit la suite des événements dans le repère du train, dont les passagers voient arriver le tunnel vers eux : le premier signal concerne cette fois la sortie de l'avant du train, avant que le second signal se déclenche lorsque l'arrière du train passe dans le tunnel. Ce dernier signal, émis après le premier, ne peut évidemment pas rejoindre l'avant du train.

Dans les deux analyses la bombe située à l'avant du train explose.

Notes et références

Notes

Références

Articles connexes

• Relativité restreinte, dilatation du temps et contraction des longueurs
• Intervalle d'espace-temps
• Calculs relativistes
• Paradoxe des jumeaux

• Portail de la physique