Insieme

In matematica, una collezione di elementi rappresenta un insieme se esiste un criterio oggettivo che permette di decidere univocamente se un qualunque elemento fa parte o no del raggruppamento. Si tratta di un concetto fondamentale della matematica moderna, a partire dal quale si è sviluppata la teoria degli insiemi. Nell'uso informale gli oggetti della collezione possono essere qualunque cosa: numeri, lettere, persone, figure, ecc., anche non necessariamente omogenei; nelle formalizzazioni matematiche gli oggetti della collezione vanno invece ben definiti e determinati.

Generalità

Il concetto di insieme è considerato primitivo e intuitivo: primitivo perché viene introdotto come nozione non derivabile da concetti più elementari; intuitivo perché viene introdotto come generalizzazione della nozione di insieme finito, che a sua volta è introdotta dall'analogia con l'esperienza sensibile di scatole che contengono oggetti materiali (tendenzialmente omogenei); questa impostazione si basa sulla convinzione che l'idea di insieme sia naturalmente presente nella mente umana.

Gli oggetti che compongono un insieme si dicono elementi di questo insieme; nel linguaggio matematico, detto ${\displaystyle {\displaystyle a}}$ un elemento dell'insieme ${\displaystyle {\displaystyle A}}$, si dice che ${\displaystyle {\displaystyle a}}$ appartiene ad ${\displaystyle {\displaystyle A}}$ o in simboli ${\displaystyle {\displaystyle a\in A}}$. Un insieme ${\displaystyle {\displaystyle A}}$ è sottoinsieme di un altro insieme ${\displaystyle {\displaystyle B}}$ quando tutti gli elementi di ${\displaystyle {\displaystyle A}}$ appartengono anche a ${\displaystyle {\displaystyle B}}$.

Ciò che caratterizza il concetto di insieme e lo differenzia da strutture matematiche simili sono essenzialmente le seguenti proprietà:

• Un elemento può appartenere o non appartenere a un determinato insieme, non ci sono vie di mezzo (come accade invece per gli insiemi sfocati);
• Un elemento non può comparire più di una volta in un insieme (mentre può comparire più volte in un multiinsieme);
• Gli elementi di un insieme non hanno un ordine di comparizione (come invece accade alle componenti di un vettore o di una ennupla);
• Gli elementi di un insieme lo caratterizzano univocamente: due insiemi coincidono se e solo se hanno gli stessi elementi.

Gli insiemi, con le loro operazioni e relazioni, possono essere rappresentati graficamente con i diagrammi di Eulero-Venn.

Descrizioni di insiemi

Solitamente un insieme viene indicato con le lettere maiuscole dell'alfabeto: ${\displaystyle {\displaystyle A}}$, ${\displaystyle {\displaystyle B}}$, ${\displaystyle {\displaystyle E}}$, ${\displaystyle {\displaystyle M}}$, ${\displaystyle {\displaystyle S}}$ ... e si chiede che sia univocamente determinato: se ad esempio diciamo che ${\displaystyle {\displaystyle M}}$ è l'insieme degli ${\displaystyle {\displaystyle x}}$ tali che ${\displaystyle {\displaystyle x}}$ è un mammifero marino, allora supponiamo che si sappia sempre decidere se un qualsiasi animale possibile e immaginabile abbia o meno le caratteristiche necessarie per rientrare in ${\displaystyle {\displaystyle M}}$. Se un oggetto ${\displaystyle {\displaystyle x}}$ appartiene ad un insieme ${\displaystyle {\displaystyle F}}$ viene detto elemento di ${\displaystyle {\displaystyle F}}$ e la relazione si denota nella forma ${\displaystyle x\in F}$. Viceversa, la relazione di non appartenenza a un insieme si denota nella forma ${\displaystyle x\notin F}$.

Un insieme può essere definito nei seguenti modi:

• Per elencazione o in estensione: sono elencati gli elementi, in tal caso per convenzione si scrivono gli elementi tra parentesi graffe separati da virgole, ad esempio:

${\displaystyle F=\{{\mbox{rosa, giglio, geranio}}\}.}$

Questa definizione si utilizza per gli insiemi finiti; per gli insiemi infiniti talvolta si usano puntini di sospensione laddove si ritiene che sia evidente il criterio secondo cui si individuano gli elementi non indicati; ad esempio:

${\displaystyle P=\left\{1,{\frac {1}{2}},{\frac {1}{3}},{\frac {1}{4}},{\frac {1}{5}},\,\dots {}\right\}}$.

• Per proprietà caratteristica o in comprensione: come l'insieme degli oggetti che verificano una determinata proprietà ${\displaystyle P}$. In tal caso si usa la scrittura ${\displaystyle {\displaystyle \{x\mid P(x)\}}}$ dove al posto di ${\displaystyle P(x)}$ può comparire la descrizione d'una proprietà. Es. : ${\displaystyle {\displaystyle F=\{x\mid x{\mbox{ è un fiore}}\}}}$ (${\displaystyle F}$ è definito come l'insieme degli ${\displaystyle {\displaystyle x}}$ tali che ${\displaystyle {\displaystyle x}}$ è un fiore), ${\displaystyle F=\left\{x\mid x={\frac {1}{n}}{\mbox{ con }}n{\mbox{ numero intero positivo}}\right\}}$.

Cardinalità

La cardinalità di un insieme è il numero che indica la quantità dei suoi elementi. Ad esempio, l'insieme ${\displaystyle \{a,b,c\}}$ ha tre elementi (considerando distinte le tre lettere), quindi cardinalità 3; l'insieme dei numeri naturali ${\displaystyle \mathbb {N} }$ ha invece cardinalità ${\displaystyle \aleph _{0}}$, il primo cardinale infinito.

Un insieme si dice finito se ha un numero finito di elementi, infinito se contiene infiniti elementi.

Operazioni tra insiemi

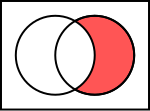
Le principali operazioni tra insiemi sono:

• L'unione di due insiemi ${\displaystyle {\displaystyle A}}$ e ${\displaystyle {\displaystyle B}}$: si indica con ${\displaystyle A\cup B}$ ed è l'insieme formato da tutti gli elementi di ${\displaystyle {\displaystyle A}}$ o di ${\displaystyle {\displaystyle B}}$ o di entrambi;

• L'intersezione di due insiemi ${\displaystyle {\displaystyle A}}$ e ${\displaystyle {\displaystyle B}}$: si indica con ${\displaystyle A\cap B}$ ed è data dall'insieme formato da tutti gli elementi che appartengono sia all'insieme ${\displaystyle {\displaystyle A}}$ che all'insieme ${\displaystyle {\displaystyle B}}$;

• La differenza tra ${\displaystyle {\displaystyle B}}$ e ${\displaystyle {\displaystyle A}}$ si indica con ${\displaystyle B\setminus A}$ o con ${\displaystyle {\displaystyle B\smallsetminus A}}$ oppure ancora con ${\displaystyle B-A}$ ed è data dall'insieme formato dai soli elementi di ${\displaystyle {\displaystyle B}}$ che non appartengono ad ${\displaystyle {\displaystyle A}}$. ${\displaystyle B\setminus A}$ viene anche detto insieme complementare di ${\displaystyle {\displaystyle A}}$ in ${\displaystyle {\displaystyle B}}$;

• La differenza simmetrica tra due insiemi è l'insieme degli elementi che appartengono ad ${\displaystyle {\displaystyle A}}$ e non a ${\displaystyle {\displaystyle B}}$ oppure che appartengono a ${\displaystyle {\displaystyle B}}$ e non ad ${\displaystyle {\displaystyle A}}$. Si indica con ${\displaystyle A\triangle B=(A\setminus B)\cup (B\setminus A)}$;

• Il prodotto cartesiano di due insiemi ${\displaystyle {\displaystyle A}}$ e ${\displaystyle {\displaystyle B}}$ è l'insieme di tutte le possibili coppie ordinate ${\displaystyle (a,b)}$ con ${\displaystyle a\in A}$ e ${\displaystyle b\in B}$.

Relazioni tra insiemi

Due insiemi ${\displaystyle {\displaystyle A}}$ e ${\displaystyle {\displaystyle B}}$ si dicono inoltre:

• Coincidenti, se sono lo stesso insieme: questo si verifica se e solo se hanno gli stessi elementi;
• Disgiunti, se non hanno nessun elemento in comune.

${\displaystyle {\displaystyle B}}$ è sottoinsieme di ${\displaystyle {\displaystyle A}}$ se ${\displaystyle {\displaystyle A}}$ contiene gli elementi di ${\displaystyle {\displaystyle B}}$. Secondo la definizione ogni insieme è contenuto in sé stesso. Per esprimere questo si usa la notazione:

${\displaystyle B\subseteq A.}$

Se si vuole escludere che ${\displaystyle {\displaystyle B}}$ coincida con ${\displaystyle {\displaystyle A}}$, cioè prevedere che esistono elementi di ${\displaystyle {\displaystyle A}}$ non contenuti in ${\displaystyle {\displaystyle B}}$, si usa la notazione:

${\displaystyle B\subset A}$

che si legge: "${\displaystyle {\displaystyle B}}$ è un sottoinsieme proprio di ${\displaystyle {\displaystyle A}}$" oppure "${\displaystyle {\displaystyle B}}$ è incluso propriamente in ${\displaystyle {\displaystyle A}}$" oppure "${\displaystyle {\displaystyle B}}$ è contenuto propriamente in ${\displaystyle {\displaystyle A}}$". Alcuni autori utilizzano solo la seconda notazione, indipendentemente dal tipo di inclusione.

La relazione binaria di inclusione tra insiemi rende una qualsiasi classe di insiemi un insieme parzialmente ordinato.

L'insieme vuoto

Insieme vuoto è l'insieme che non contiene nessun elemento. Si indica con i simboli ${\displaystyle \varnothing }$, ${\displaystyle \emptyset }$ o con due parentesi graffe, la prima aperta e l'altra chiusa ${\displaystyle \left\{\right\}}$.

L'insieme vuoto è sottoinsieme di qualsiasi altro insieme (incluso sé stesso).

L'insieme delle parti

Per qualunque insieme ${\displaystyle {\displaystyle A}}$ si definisce insieme delle parti o "insieme potenza" di ${\displaystyle {\displaystyle A}}$ e si indica con ${\displaystyle {\mathcal {P}}(A)}$ o ${\displaystyle 2^{A}}$ l'insieme che ha come elementi tutti e soli i sottoinsiemi di ${\displaystyle {\displaystyle A}}$. Ad esempio, se ${\displaystyle A=\left\{a,b,c\right\}}$ allora il suo insieme delle parti è costituito da ${\displaystyle {\mathcal {P}}(A)=\{\emptyset ,\{a\},\{b\},\{c\},\{a,b\},\{a,c\},\{b,c\},A\}}$.

L'insieme delle parti ha cardinalità strettamente maggiore di quella dell'insieme di partenza. Se ${\displaystyle {\displaystyle A}}$ è finito e ha ${\displaystyle {\displaystyle |A|}}$ elementi, il numero degli elementi di ${\displaystyle {\mathcal {P}}(A)}$ è dato da ${\displaystyle 2^{|A|}}$ (in simboli, ${\displaystyle |{\mathcal {P}}(A)|=|2^{A}|=2^{|A|}}$).

L'insieme delle parti di qualsiasi insieme, considerato congiuntamente all'operazione di differenza simmetrica, forma un gruppo abeliano. Se vengono considerate insieme unione, intersezione e complementazione la struttura generata è un'algebra di Boole.

La partizione di un insieme

Si chiama partizione dell'insieme ${\displaystyle A}$ un insieme di sottoinsiemi di ${\displaystyle A}$ che ha queste caratteristiche:

• ogni sottoinsieme non è vuoto;
• tutti i sottoinsiemi sono disgiunti tra loro;
• l'unione di tutti i sottoinsiemi è ${\displaystyle A.}$

L'insieme complementare di un insieme

Dati gli insiemi ${\displaystyle A}$ e ${\displaystyle B,}$ con ${\displaystyle B\subseteq A}$, l'insieme complementare di ${\displaystyle B}$ rispetto ad ${\displaystyle A}$ è ${\displaystyle {\displaystyle A\smallsetminus B}}$ Lo indichiamo con ${\displaystyle {\displaystyle C_{A}(B).}}$

Insiemi numerici

Alcuni insiemi, detti numerici, hanno un ruolo particolarmente importante e pervasivo in tutte le branche della matematica:

• L'insieme ${\displaystyle \mathbb {N} }$ dei numeri naturali.
• L'insieme ${\displaystyle \mathbb {Z} }$ dei numeri interi.
• L'insieme ${\displaystyle \mathbb {Q} }$ dei numeri razionali.
• L'insieme ${\displaystyle \mathbb {R} }$ dei numeri reali.
• L'insieme ${\displaystyle \mathbb {C} }$ dei numeri complessi.

Questi insiemi si possono vedere intuitivamente come contenuti uno nell'altro:

${\displaystyle \mathbb {N} \subset \mathbb {Z} \subset \mathbb {Q} \subset \mathbb {R} \subset \mathbb {C} .}$

Più propriamente si dovrebbe parlare di immersione di ogni insieme nel seguente, poiché secondo la corrente assiomatizzazione i vari insiemi sono definiti in modi radicalmente diversi l'uno dall'altro. Dunque non si può dire che ${\displaystyle \mathbb {N} }$ sia contenuto in ${\displaystyle \mathbb {Z} }$, ma che vi sia una funzione iniettiva da ${\displaystyle \mathbb {N} }$ a ${\displaystyle \mathbb {Z} }$.

Note

Bibliografia

• Serge Lang, Algebra lineare, Torino, Bollati Boringhieri, 1992.
• Seymour Lipschutz, Topologia, Sonzogno, Etas Libri, 1979.
• (EN) Paul Halmos (1960): Naive set theory, D. Van Nostrand Company. Ristampato da Springer nel 1974, ISBN 0-387-90092-6.
• (FR) Nicolas Bourbaki (1968): Théorie des ensembles, Hermann.

Voci correlate

• Teoria degli insiemi
• Teoria ingenua degli insiemi
• Teoria assiomatica degli insiemi
• Set (informatica)

Altri progetti

• Wikiquote contiene citazioni sull'insieme
• Wikizionario contiene il lemma di dizionario «insieme»
• Wikiversità contiene risorse sull'insieme
• Wikimedia Commons contiene immagini o altri file sull'insieme

Collegamenti esterni

• insieme, su Treccani.it – Enciclopedie on line, Istituto dell'Enciclopedia Italiana.
• insième, su Vocabolario Treccani, Istituto dell'Enciclopedia Italiana.
• insième, su sapere.it, De Agostini.
• (EN) set, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Set, su MathWorld, Wolfram Research.

V · D · M Teoria degli insiemi
Insiemi numerici	Naturali · Interi · Razionali · Reali · Complessi
Teoria ingenua degli insiemi (o di Cantor)	Insieme vuoto · Insieme universo · Sottoinsieme · Insieme potenza · Insieme complemento · Unione · Intersezione · Coppia ordinata · Prodotto cartesiano · Paradosso di Russell · Paradosso di Burali-Forti
Teoria assiomatica degli insiemi	Assioma · Assiomi di Peano · Teoria degli insiemi di Zermelo · Teoria degli insiemi di Zermelo-Fraenkel · Assioma della scelta · Lemma di Zorn · Teoria degli insiemi di Von Neumann-Bernays-Gödel

Controllo di autorità	Thesaurus BNCF 5501 · GND (DE) 4038613-2