Fibrato

Disambiguazione – Se stai cercando gli omonimi farmaci ipolipidemizzanti, vedi fibrati.
Una spazzola cilindrica illustra intuitivamente il concetto di fibrato. La spazzola rappresenta un fibrato dove la base è un cilindro e le fibre (setole) sono i segmenti. L'applicazione π : E → B {\displaystyle \scriptstyle {\pi \colon E\to B}} manda un punto di ogni setola nel punto del cilindro dove la setola è attaccata.

In matematica, e più precisamente in topologia, un fibrato è una particolare funzione π : E → B {\displaystyle \pi :E\to B} che si comporta localmente come la proiezione di un prodotto su un fattore.

I fibrati sono utili in topologia differenziale e in topologia algebrica. Un esempio importante di fibrato è il fibrato tangente. Sono anche uno strumento importante nella teoria di gauge.

Definizione

Un fibrato è una funzione suriettiva continua fra spazi topologici π : E → B {\displaystyle \pi :E\to B} che è localmente un prodotto. Più precisamente, fissato uno spazio topologico F {\displaystyle F} , ogni punto x {\displaystyle x} di B {\displaystyle B} possiede un intorno aperto U {\displaystyle U} tale che la controimmagine π − 1 ( U ) {\displaystyle \pi ^{-1}(U)} è omeomorfa al prodotto U × F {\displaystyle U\times F} , e la π {\displaystyle \pi } letta su questo prodotto è la proiezione sul primo fattore. In altre parole, il seguente diagramma commuta:

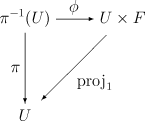
Local triviality condition

dove p r o j 1 : U × F → U {\displaystyle {\mathrm {proj} }_{1}\colon U\times F\to U} è la naturale proiezione sul primo fattore e ϕ : π − 1 ( U ) → U × F {\displaystyle \phi \colon \,\pi ^{-1}(U)\to U\times F} è un omeomorfismo. L'insieme di tutti gli omeomorfismi { ( U i , ϕ i ) } {\displaystyle \{(U_{i},\phi _{i})\}} si dice trivializzazione locale del fibrato.

Lo spazio B {\displaystyle B} è la base o spazio di base, F {\displaystyle F} è la fibra, E {\displaystyle E} è lo spazio totale e π {\displaystyle \pi } la proiezione. Il fibrato è a volte denotato nel modo seguente:

F ⟶ E   →   π     B {\displaystyle F\longrightarrow E\ {\xrightarrow {\,\ \pi \ }}\ B}

Un fibrato è differenziabile (o liscio) se è definito nella categoria delle varietà differenziabili: E , B {\displaystyle E,B} e F {\displaystyle F} in questo caso sono varietà differenziabili e le π , ϕ {\displaystyle \pi ,\phi } sono funzioni differenziabili.[1] In particolare, ogni fibrato differenziabile è una varietà fibrata.

Esempi

Prodotto

Il prodotto topologico E = B × F {\displaystyle E=B\times F} di due spazi è, con la proiezione sul primo fattore, un fibrato sopra la base B {\displaystyle B} a fibra F {\displaystyle F} . Un tale fibrato è detto banale (o triviale). Si dimostra che ogni fibrato sopra uno spazio cellulare contrattile è banale.

Nastro di Möbius

Il nastro di Möbius è un fibrato non banale sulla circonferenza.

Il nastro di Möbius è forse l'esempio più semplice di fibrato non banale. La base B {\displaystyle B} consiste in una circonferenza, e la fibra F {\displaystyle \scriptstyle {F}\,} è un segmento. Dato x {\displaystyle x} in B {\displaystyle B} , un piccolo arco U {\displaystyle U} della circonferenza contenente x {\displaystyle x} ha effettivamente come controimmagine un rettangolo U × F {\displaystyle U\times F} . Globalmente, il nastro di Möbius non è però un prodotto B × F {\displaystyle B\times F} : un tale prodotto sarebbe infatti una corona circolare.

Toro e bottiglia di Klein

Un toro.
La bottiglia di Klein immersa nello spazio tridimensionale.

Analogamente, il toro è un prodotto S 1 × S 1 {\displaystyle S^{1}\times S^{1}} fra due circonferenze S 1 {\displaystyle S^{1}} , mentre la bottiglia di Klein è un altro fibrato, avente sempre base S 1 {\displaystyle S^{1}} e fibra S 1 {\displaystyle S^{1}} .

Rivestimenti

Un rivestimento è un fibrato in cui la proiezione è un omeomorfismo locale. In particolare, la fibra è un insieme discreto di punti.

Fibrati vettoriali

Lo stesso argomento in dettaglio: Fibrato vettoriale.

Un fibrato vettoriale è un fibrato la cui fibra F {\displaystyle F} è uno spazio vettoriale. I fibrati vettoriali occupano un ruolo centrale in topologia e in geometria algebrica. L'esempio più importante di fibrato vettoriale è il fibrato tangente.

Fibrazione di Hopf

Lo stesso argomento in dettaglio: Fibrazione di Hopf.

La fibrazione di Hopf è un particolare fibrato fra sfere f : S 3 → S 2 {\displaystyle f:S^{3}\to S^{2}} avente come fibra S 1 {\displaystyle S^{1}} .

Proprietà

Mappa aperta

La proiezione π {\displaystyle \pi } è sempre una funzione aperta.

Sezioni

Lo stesso argomento in dettaglio: Sezione (geometria differenziale).

Una sezione di un fibrato è una funzione continua

s : B → E {\displaystyle s:B\to E\,\!}

tale che π ( s ( x ) ) = x {\displaystyle \pi (s(x))=x} per ogni x {\displaystyle x} in B {\displaystyle B} . Ad esempio, in un fibrato banale E = F × B {\displaystyle E=F\times B} , preso un punto y 0 {\displaystyle y_{0}} in F {\displaystyle F} , si può definire la sezione

s ( x ) = ( y 0 , x ) . {\displaystyle s(x)=(y_{0},x).}

Un generico fibrato può ammettere o non ammettere sezioni. L'esistenza di una sezione conduce alla definizione delle classi caratteristiche.

Molti oggetti comunemente incontrati nelle teorie matematiche e fisiche possono essere formalizzati come sezioni di un particolare fibrato, di sovente vettoriale. Ad esempio, un campo vettoriale è una sezione del fibrato tangente. Una forma differenziale o un più generico campo tensoriale (come ad esempio il tensore di Riemann) sono anch'essi sezioni di una tipologia di fibrati vettoriali, noti col nome di fibrati tensoriali. Infine, i campi che costituiscono gli oggetti di studio delle teorie di campo classiche possono essere formalizzati come sezioni di particolari fibrati vettoriali, come avviene ad esempio con gli spinori nelle teorie di campo a spin 1/2.

Note

  1. ^ (EN) I. Kolář, P. Michor, J. Slovák, Natural operators in differential geometry (PDF), Springer-Verlag, 1993, pp. 76-77. URL consultato il 3 luglio 2013 (archiviato dall'url originale il 30 marzo 2017).

Bibliografia

  • (EN) I. Kolář, P. Michor, J. Slovák, Natural operators in differential geometry (PDF), Springer-Verlag, 1993. URL consultato il 3 luglio 2013 (archiviato dall'url originale il 30 marzo 2017).
  • (EN) Dale Husemöller, Fibre Bundles, Springer Verlag, 1994, ISBN 0-387-94087-1.
  • (EN) Norman Steenrod, The Topology of Fibre Bundles, Princeton University Press, 1951, ISBN 0-691-08055-0.

Voci correlate

Controllo di autoritàLCCN (EN) sh85048011 · J9U (EN, HE) 987007531250205171 · NDL (EN, JA) 00562768
  Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica